1. Пусть 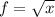 ,
, 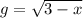 . Заметим, что
. Заметим, что 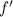 и
и 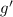 монотонно убывают, значит,
монотонно убывают, значит, 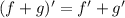 функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения
функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения 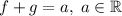 не более двух корней.
не более двух корней.
2. Заметим, что если 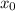 является решением, то
является решением, то  тоже. Очевидно, что
тоже. Очевидно, что 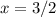 является осью симметрии (причем единственной) графика
является осью симметрии (причем единственной) графика 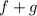 . Иначе говоря, пара
. Иначе говоря, пара 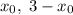 исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы
исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы 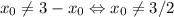 . Итак,
. Итак, 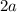 пробегает область значения рассматриваемой функции, кроме того
пробегает область значения рассматриваемой функции, кроме того  , которому соответствует
, которому соответствует 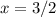 (это
(это 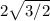 ).
).
3. Функция непрерывна, поэтому достаточно посмотреть на наименьшее и наибольшее значения. Наименьшее значение достигается в 0 (то есть значение 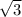 , а наибольшее в
, а наибольшее в 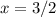 . Получаем ответ:
. Получаем ответ: 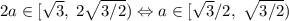

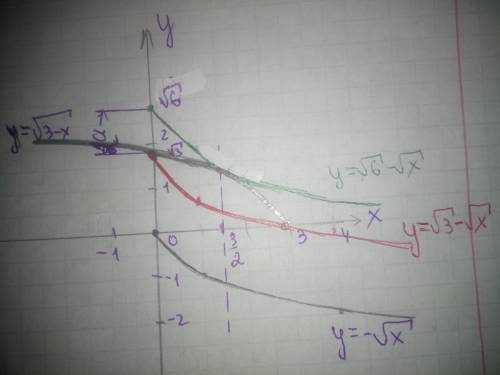
Угол α наклона к оси Ох касательной к графику функции при х = 2 равен:
α = arc tg 2 = 1,107149 радиан = 63,43495°.
2) Если производная некоторой функции на интервале (1, 5) постоянна и равна 2, то и функция на этом промежутке совпадает с касательной. Уравнение касательной у = кх + в имеет положительное значение коэффициента к = 2, то есть прямая возрастающая, значит, и функция возрастает.
3) Имеет ли функция y = 1 – x² локальный минимум?
Нет, не имеет.
График её - парабола ветвями вниз, не имеет локального минимума.