Наибольший общий делитель (НОД) двух данных чисел 21 и 35 — это наибольшее число, на которое оба числа 21 и 35 делятся без остатка.
НОД (21; 35) = 7.
Как найти наибольший общий делитель для 21 и 35
Разложим на простые множители 21
21 = 3 • 7
Разложим на простые множители 35
35 = 5 • 7
Выберем одинаковые простые множители в обоих числах.
7
Находим произведение одинаковых простых множителей и записываем ответ
НОД (21; 35) = 7 = 7
НОК (Наименьшее общее кратное) 21 и 35
Наименьшим общим кратным (НОК) 21 и 35 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (21 и 35).
НОК (21, 35) = 105
Как найти наименьшее общее кратное для 21 и 35
Разложим на простые множители 21
21 = 3 • 7
Разложим на простые множители 35
35 = 5 • 7
Выберем в разложении меньшего числа (21) множители, которые не вошли в разложение
3
Добавим эти множители в разложение бóльшего числа
5 , 7 , 3
Полученное произведение запишем в ответ.
НОК (21, 35) = 5 • 7 • 3 = 105
Теперь все это складываем:
105 + 7 = 112
ответ: 112
наверно ты имела ввиду что надо составить плоскость в которой лежат все три эти точки, привести его к общему виду и к виду в отрезках.
Чтобы найти уравнение плоскости, необходимо составить определитель вида
![\left[\begin{array}{ccc}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\\x_{3}-x_{1}&y_{3}-y_{1}&z_{3}-z_{1}\\x-x_{1}&y-y_{1}&z-z_{1}\end{array}\right] =0](/tpl/images/0112/1221/de396.png) :
:
где соответствующие координаты принадлежать соответствующим точкам. Получаем:
![\left[\begin{array}{ccc}-1-1&0-2&4+1\\-2-1&-1-2&1+1\\x-1&y-2&z+1\end{array}\right] =0 \\ \\ \\ \left[\begin{array}{ccc}-2&-2&5\\-3&-3&2\\x-1&y-2&z+1\end{array}\right] =0 \\ \\ \\](/tpl/images/0112/1221/0862b.png)
Раскрываем определитель
![-2\left[\begin{array}{cc}-3&2\\y-2&z+1\end{array}\right] +2\left[\begin{array}{cc}-3&2\\x-1&z+1\end{array}\right] + 5\left[\begin{array}{cc}-3&-3\\x-1&y-2\end{array}\right] = 0](/tpl/images/0112/1221/569c5.png)
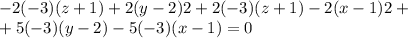
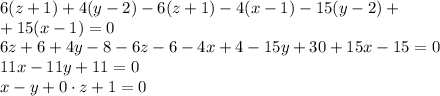 ]
]
x-y+1 = 0 Искомое уравнение плоскости, из-за коэфициента при координате z равного нулю, координата z не учитывается в уравнении. Плоскость параллельна оси Оz.
Приведем уравнение плоскости из общего вида к виду в отрезках. Уравнение в отрезках имеет вид
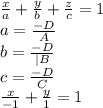
72:9=8