Пошаговое объяснение:1) f(x)= 2x²-3x+1 , [-1;1] ⇒ f'(x)= 4x-3, найдём критические точки: 4х-3=0, ⇒ х = 3/4=0,75 ∈[-1;1]. Найдём значения функции в критической точке и на концах данного промежутка: f(3/4)= 2·(3/4)²- 3·3/4 +1 =9/8 -9/4 + 1 = -1/8 ; f(1) = 0; f(-1)=6 ⇒ max f(x)=f(-1)=6; minf(x)=f(3/4)=-1/8
2)f(x)=3x²-4 на [2;4] ⇒ f'(x)=6x 6x=0, x=0-крит. точка, но x=0∉ [2;4] ⇒ Найдём значения функции на концах данного промежутка: f(2)= 3·2²-4= 12-4=8 f(4)=3·4² - 4= 48-4=44 ⇒ max f(x)=f(-4)=44; minf(x)=f(2)=8 3)f(x)=x²-1 на [0;3]⇒ f'(x)=2x , 2x=0 x=0 -критическая точка х=0 ∈ [0;3]. Найдём значения функции в критической точке и на концах данного промежутка: f(0) =0²-1=-1; f(3)=3²-1=8 ⇒max f(x)=f(3)=8; minf(x)=f(0)= -1
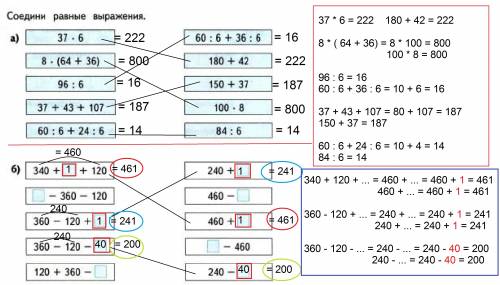
преобразовываем 340 + ... + 120 = 460 + ....
в правом столбике есть 460 + ...
то есть подставив одинаковые числа ( любые), получаем одинаковые значения.
360 - 120 + .... = 240 + ..... правый столбик 240 + ......
( вместо точек ставим одинаковые числа, получаем одинаковые значения)
360 - 120 - ... = 240 - .... правый столбик 240 - .....
тоже вместо точек одинаковые числа (любое от 0 до 240)
.................................................................................................
больше нет выражений, преобразовав которые мы получим " правый столбик"
1)5а+3а-7а-2а = 8а-9а= -а
2) -4b + 5b-6b+3b = 8b-10b= -2b
3) 2,8x+3,5x-1,8x-2,5x = 2,8x -1,8x + 3,5x -2,5x= 1x+ 1x= 2x
4) 3 2/11x + 2 3/7x - 1 2/11x - 1 3/7x=
3 2/11x - 1 2/11x + 2 3/7x - 1 3/7x =
2x + 1x= 3x
{1 обычно не пишем); считаем числа возле букв, как в примерах. Если буквы разные или просто цифры то их раздельно считаем;