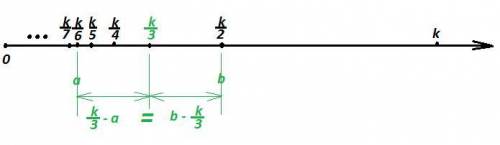
Расположим делители числа k в порядке возрастания (естественно, если такие делители существуют).
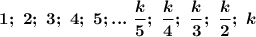
Пусть a < b.
Так как различные натуральные делители a и b расположены на одинаковом расстоянии от числа k/3, то расположены они по разные стороны от числа k/3
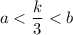
На числовой оси правее числа k/3 ( то есть больше числа k/3) расположены только два делителя : само число k и k/2.
b = k не подходит по условию, так как делитель a тогда отрицательный
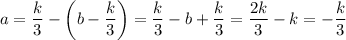
Остаётся единственный вариант 
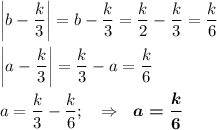
Так как у делителей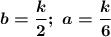 
общий знаменатель равен 6, то олимпиадными будут все числа, кратные 6. Тогда олимпиадных чисел, не превосходящих 2018:
2018 : 6 = 336,(3) - 336 чисел
Проверка :
k=6; b=3; a=1; |1-2|=|3-2| =1
k=12; b=6; a=2; |2-4|=|6-4| =2
k=18; b=9; a=3; |3-6|=|9-6| =3 ...
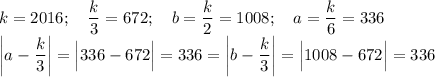
ответ : 336 чисел
1) p=3;
2) p>3.
Пошаговое объяснение:
Количество корней квадратного уравнения зависит от дискриминанта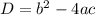 
, где a, b и c - коэффициенты в исходном уравнении (
)
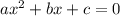Для данного уравнения:
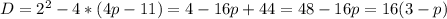
Уравнение имеет 2 совпадающих корня, если дискриминант равен нулю, и не имеет решений в действительных числах, если дискриминант отрицательный.
1) 16(3-p)=0, p=3;
2) 16(3-p)<0, p>3.
Также первый ответ можно получить другим Если квадратное уравнение имеет 2 равных корня, значит, это квадрат суммы.
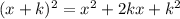, сравнивая с исходным уравнением, получаем, что k=1, 4p-11=1, отсюда p=3.
100+110=210км/ч( общая)
840÷210=4ч
ответ через 4часа