ясно, что двигаясь вниз и вправо, независимо от формы пути, фоксу нужно будет сделать 6 ходов, чтобы из левой верхней клетки попасть в правую нижнюю. из этих шести ходов 3 обязательно будут на одну клетку вниз, а 3 - на одну клетку вправо. поскольку после каждого ходачисло под фишкой меняется, то имеем перестановку из 6 элементов двух разных типов, по три каждого типа. чтобы подсчитать общее количество вариантов достижения правой нижней клетки применяем формулу для числа перестановок n элементов с повторениями:
p = n! / (n1! где n=6; n1=3 и n2=3.
подставляя, получаем
p=6! / (3! 3! )=720/36=20
ответ: 20
Найдем сначала общее решение соответствующего однородного дифференциального уравнения
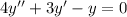
Пусть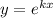 
, мы получим характеристическое уравнение
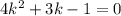
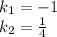
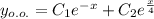— общее решение однородного диф. ур.
Найдём теперь частное решение. Рассмотрим функцию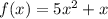 
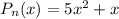отсюда 
; 
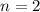. Сравнивая 
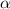с корнями характеристического уравнения и, принимая во внимая, что , частное решение будем искать в виде:
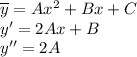
Подставляем в исходное дифференциальное уравнение
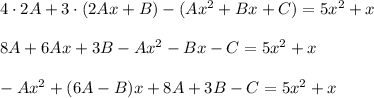
Приравниваем коэффициенты при степени x
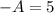откуда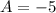 
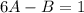откуда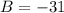 
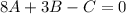откуда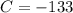 
Частное решение: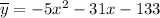 
Общее решение линейного неоднородного дифференциального уравнения:
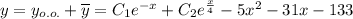
Волга является важной судоходной артерией впадающей в каспийское море.
Волга являлась кормилицей русского народа. Потом она была как источник гидрэлектроэнергии.
Волга протекает в европейской части России,именно там зародилась основная масса русского народа. Значит река является своеобразным символом русского народа.