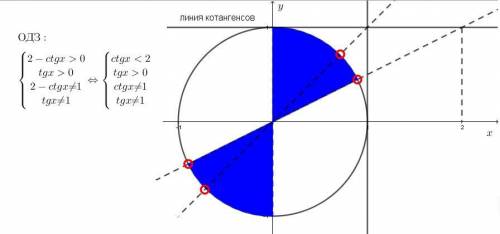
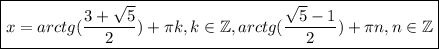ОДЗ на рисунке (решения долны входить в синие секторы)
решение на фото.
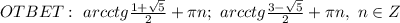
 " />
" /> " />
" />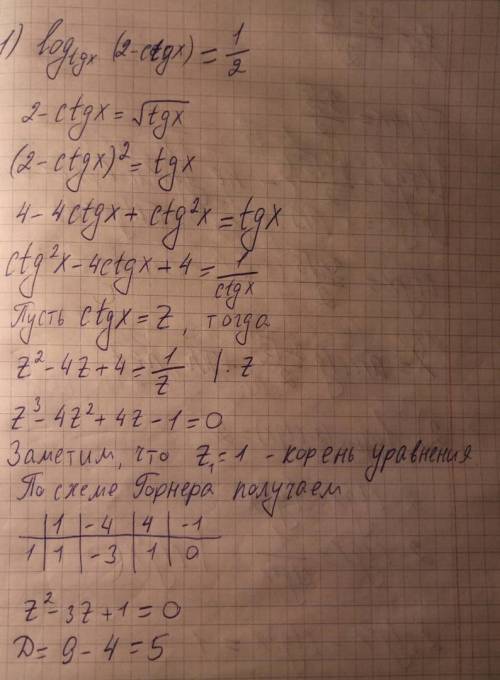 " />
" />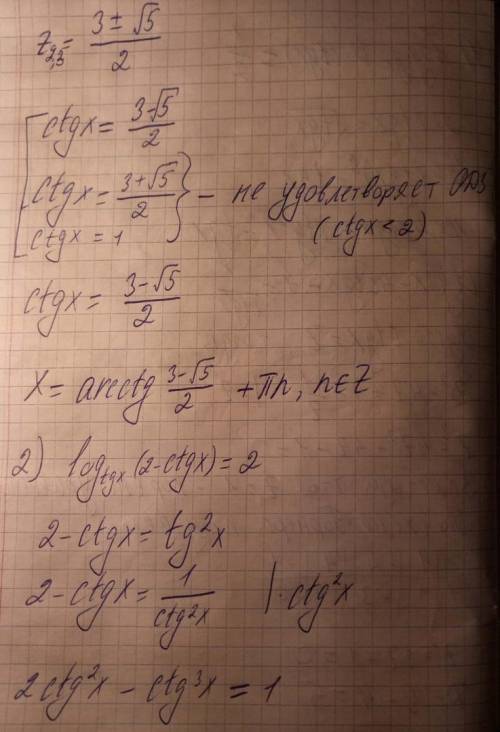 " />
" />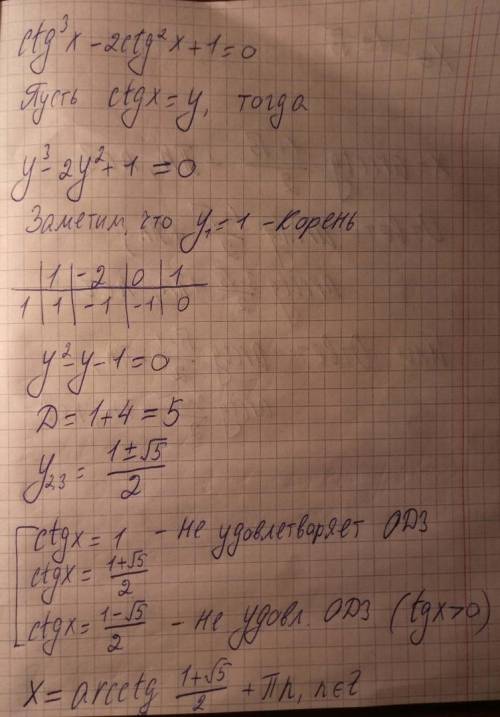 " />
" />
ответ:
симметрия в природе
целью данной работы является определение роли симметрии в живой и неживой природе.
симметрия является одной из наиболее и одной из наиболее общих закономерностей мироздания: живой, неживой природы и общества. принципы симметрии играют важную роль в и , и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке.
законы природы, неисчерпаемой в своем многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
существует две группы симметрии. к первой группе относится симметрия положений, форм, структур. это та симметрия, которую можно непосредственно видеть. она может быть названа симметрией. вторая группа характеризует симметрию явлений и законов природы. эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать симметрией.
исследование симметрии земли как планеты в целом позволяет систематически и с соответствующей детальностью проанализировать динамику формирования фигуры земли, т. е. рассмотреть качественную и количественную роль различных силовых полей, воздействие которых определяет эту фигуру.
суммарное воздействие силы земного тяготения можно изобразить в виде пучка бесчисленного множества одинаковых векторов, направленных к одной общей точке – центру земли. симметрия такого пучка, так же как и симметрия идеального и неподвижного шара отвечает бесчисленному множеству осей симметрии бесконечного порядка (осей вращения) и бесчисленному множеству плоскостей симметрии, пересекающихся в одной точке – центре шара. симметрия воздействующего на землю поля солнечной радиации соответствует, очевидно, симметрии конуса, ось которого совпадает с осью солнце – земля. поле солнечной радиации в окрестностях земли – симметрия цилиндра.
круговая симметрия обладает большой общностью. главная особенность кругового преобразования состоит в том, что оно всегда сохраняет углы фигуры и сферу, и всегда переходит в сферу другого радиуса. вот почему кристаллы любого вещества могут иметь самый разный вид, но углы между гранями всегда постоянны. каждая снежинка – это маленький кристалл замерзшей воды. форма снежинок может быть разнообразной, но все они симметрией – поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
на явление симметрии в живой природе обратили внимание еще пифагорейцы в связи с развитием ими учения о гармонии. установлено, что в природе наиболее распространены два вида симметрии - «зеркальная» и «лучевая» (или «радиальная») симметрии.
у цветковых растений в большинстве проявляется радиальная и зеркальная симметрия. цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей. к формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево и часто такой вид симметрии называется «ромашко-грибной» симметрией. для листьев характерна зеркальная симметрия.
типы симметрии у животных: центральная; осевая; радиальная; билатеральная (зеркальная); поступательная и поступательно-вращательная; винтовая, а также спиральная симметрия. примером винтовой симметрии может служить раковина улитки (правый винт). зеркальная симметрия хорошо видна у бабочки; симметрия левого и правого проявляется здесь с почти строгостью.
также отметим зеркальную симметрию человеческого тела: правое и левое полушария головного мозга, правые и левые кисти рук, ступни ног и т.д. она же проявляется в гармонии человеческих движений, как в танцах, так и в технической работе, где проявляется закономерность.
принципы симметрии лежат в основе теории относительности, квантовой механики, твердого тела, атомной и ядерной , элементарных частиц. эти принципы наиболее ярко выражаются в свойствах инвариантности законов природы. речь при этом идет не только о законах, но и других, например, биологических. примером биологического закона сохранения может служить закон наследования. молекула днк, являющаяся носителем наследственной информации в живом организме, имеет структуру двойной правой спирали.
принцип «симметрии» широко используется в искусстве. бордюры, используемые в архитектурных и скульптурных произведениях, орнаменты, используемые в прикладном искусстве, - все это примеры использования симметрии.
на основании вышесказанного можно утверждать, симметрия в природе проявляется в самых различных объектах материального мира и отражает наиболее общие, наиболее его свойства. поэтому исследование симметрии разнообразных природных объектов и сопоставление результатов является удобным и надежным инструментом познания основных закономерностей существования материи. без принципа симметрии нельзя рассмотреть ни одной проблемы, будь то проблема жизни или проблема контактов с внеземными цивилизациями.
Объяснения:В жизни у всех нас и в нашем мире много чего интересного и прекрасного. И так одно из чего-то прекрасного - это чудо.Людям сложно объяснить это понятие. Чудом может быть как и друзей так и что-то невероятное. Но чудо это хорошие слово чудо..Разные ситуации могут даже быть опасными или же наоборот. У меня случилось один раз чудо: когда я хотела выйти на улицу сразу же пошёл дождьЯ не знала что делать ,и потом самой себе сказала дождь прикратись ,а он сразу же Или же когда машина с невероятной скоростью ехала прямо на меня ,но тут вдруг ко мне человек подбижал схватил меня за руку и прижал к себе говоря больше так не делай разве это не чудо. Неоткуда взялся человек и мне жизнь?Чудеса всегда есть но в них нужно верить и тогда чудо обязательно сбудется!
Область определения запишем
Систематизируем немного
Из последнего видим, что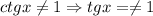 , а это уже есть. Остается тогда
, а это уже есть. Остается тогда
Правда, решая неравенство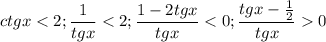
методом интервалов, получаем
Но тангенс из другого неравенства больше нуля, поэтому
Теперь решаем неравенство:
Тут t явно не равно нулю в числителе, поэтому это ограничение нам особо не нужно.
Решаем 1-ое уравнение (t=1/2):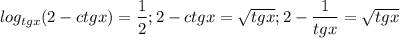
Видно по сумме коэффициентов, равно 0, что p=1 - корень уравнения. Однако,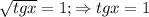 , но по ограничениям не подходит. Теперь делим уголком или по схеме Горнера на p-1 и получаем
, но по ограничениям не подходит. Теперь делим уголком или по схеме Горнера на p-1 и получаем
Видно, что оба значения положительны, но второе и больше 1/2, так как в числителе число, куда больше, чем 1.
А вот другой корень проверим:
Решаем второе уравнение:
(то, что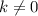 здесь понятно, поэтому смело на него умножаем все уравнение без потери корней)
здесь понятно, поэтому смело на него умножаем все уравнение без потери корней)
Тут сумма коэффициентов равна 0, k=1 - корень. Поделим на k-1 уголком или по схеме Горнера и получим
Корень k=1=tgx нам не подходит, так как по ограничениям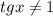
Решаем квадратное уравнение, которое дает нам вторая скобка.
Отрицательный корень не берем, так как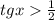
Проверим положительный корень на выполнение ограничений (сравня с 1/2)
Левое выражение больше правого, значит, этот корень удовлетворяет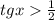 (так как
(так как 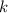 это не целое число, то оно не равно 1, то есть
это не целое число, то оно не равно 1, то есть 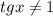 , поэтому корень подходит)
, поэтому корень подходит)
ответ: