Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: 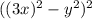 ; В следующих двух слагаемых вынесем общий множитель "40":
; В следующих двух слагаемых вынесем общий множитель "40":  ; В итоге получим следующее уравнение:
; В итоге получим следующее уравнение: 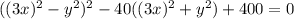 . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо
. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо  будет стоять
будет стоять  ; Это приведет к тому, что придется убавить
; Это приведет к тому, что придется убавить 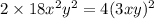 ; В итоге:
; В итоге: 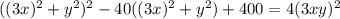 ; Слева стоит квадрат суммы. Уравнение примет вид:
; Слева стоит квадрат суммы. Уравнение примет вид:  ; Сворачивая еще раз:
; Сворачивая еще раз: 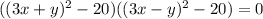 ; Получаем серию прямых:
; Получаем серию прямых:  ; А теперь приступим к рассмотрению первого уравнения.
; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом  ; Рассмотрим прямую
; Рассмотрим прямую 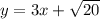 ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников.
; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 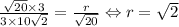 ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты
; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 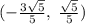 ; Ну а все решения:
; Ну а все решения:

Специальные тесты «Алпомиш» и «Барчиной» являются программной и нормативной основой системы физического воспитания населения Узбекистана. Посредством контрольных нормативов определяется общий уровень физической подготовки населения к учебной, трудовой деятельности и военной службе. Тесты укреплению здоровья, повышению творческой и трудовой активности.
Тесты «Алпомиш» предназначаются для мужской части населения, «Барчиной» - для женщин.
Тесты являются средством пропаганды здорового образа жизни, привлечения учащихся к специальным занятиям физической культурой и спортом, удовлетворения его потребностей в укреплении своего здоровья и повышения уровня физической подготовленности на различных этапах жизни. Тесты также овладению основными знаниями и практическими навыками самостоятельных занятий физическими упражнениями, содействуют использованию разнообразных форм физического упражнений в режиме учебы, труда и отдыха, а также развитию массового спорта с целью выявления и воспитания спортивных талантов.
Тесты в целях определения физической подготовленности учащихся включают в себя виды испытаний, отражающих силу, выносливость, быстроту и ловкость.
Тесты включают следующие нормативы:
Бег 30,60,100 м.
Бег 1000,2000 м.
Прыжки в длину с места и с разбега.
Метание мяча.
Бег на выносливость в течение 6 мин.
Челночный бег 4х10 м.