Пошаговое объяснение:
В основном используется табличный интеграл от степенной функции, да ещё от синуса.
\int\limits {x^n} \, dx = \frac{1}{n+1} x^{n+1} +C \\ \\ \int\limits {sinx} \, dx = -cosx + C
1а. f(x)=2-x
\int\limits {(2-x)} \, dx = 2* \frac{1}{0+1} x^{0+1} - \frac{1}{1+1}x^{1+1} + C = 2x - \frac{1}{2} x^2 +C
2б. f(x)=x^4 - sin x
\int\limits {(x^4 - sin x)} \, dx = \frac{1}{4+1}x^{4+1} -(-cosx) +C = \frac{1}{5} x^5+ cosx +C
2в. f(x)= 2/ x^3
\int\limits { \frac{2}{x^3} } \, dx = \int\limits { 2x^{-3} \, dx = 2* \frac{1}{-3+1} x^{-3+1} + C = -x^{-2} + C = - \frac{1}{x^2} + C
Пошаговое объяснение:
В основном используется табличный интеграл от степенной функции, да ещё от синуса.
\int\limits {x^n} \, dx = \frac{1}{n+1} x^{n+1} +C \\ \\ \int\limits {sinx} \, dx = -cosx + C
1а. f(x)=2-x
\int\limits {(2-x)} \, dx = 2* \frac{1}{0+1} x^{0+1} - \frac{1}{1+1}x^{1+1} + C = 2x - \frac{1}{2} x^2 +C
2б. f(x)=x^4 - sin x
\int\limits {(x^4 - sin x)} \, dx = \frac{1}{4+1}x^{4+1} -(-cosx) +C = \frac{1}{5} x^5+ cosx +C
2в. f(x)= 2/ x^3
\int\limits { \frac{2}{x^3} } \, dx = \int\limits { 2x^{-3} \, dx = 2* \frac{1}{-3+1} x^{-3+1} + C = -x^{-2} + C = - \frac{1}{x^2} + C
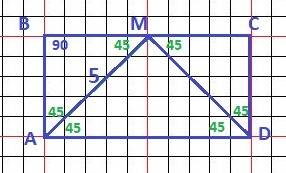
Из точки М опустим перпендикуляр MN на сторону АD. Углы ∠BMA = ∠AMN = 45°.
Треугольники ΔABM = ΔAMN по общей стороне и двум углам, прилегающим к ней. Аналогично, равны ΔMCD = ΔMDN.
Как видим на рисунке, прямоугольник ABCD превращается в квадрат AMDM1 со стороной 5 см. Следовательно, его площадь равна 25 см².
ответ: 25