До чего ленивая молодежь пошла, им уже даже пишут, какие правила использовать, а они... Не учатся ничему и учиться не хотят... :)
Пошаговое объяснение:
1) Производная произведения: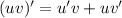 
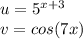
Правило дифференцирования сложной функции: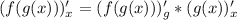
(индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
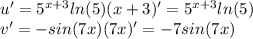
тогда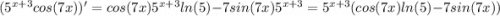 
2) Дифференцирование сложной функции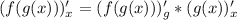
Примем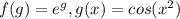 
Дифференцируем f(g):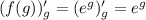 
Дифференцируем g(x): 
Тогда
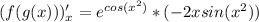
3) Как и в 2, дифференцируем сложную функцию
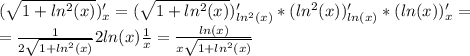
4) Производная суммы есть сумма производных:
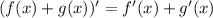
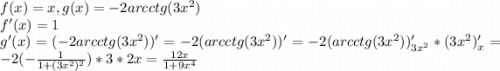
Окончательно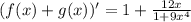 
5) Опять производная сложной функции:
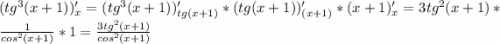
-(2+3x⁵)/x³
28x⁶-2sinx
x+5cos5x
6+3/(2(1-3x)^(3/2))
Пошаговое объяснение:
a. 1/x²-x³=d/dx(1/x²)-d/dx(x³)=-2x⁻³-3x²=-2/x³-3x²=-(2+3x⁵)/x³
b. 4x⁷+2cosx=4*(d/dx(x⁷))+2*d/dx(cosx))=4*7x⁶+2*(-d/dx(x)sinx)=28x⁶-2sinx
d/dx(cosx)=(dcosu)/du * du/dx
u=x
d/du(cosu)=-sinu
d/dx(x)=1
c. x²/2+sin5x=1/2*(d/dx(x²))+d/dx(sin(5x))=1/2*(2x)+cos(5x)*(d/dx(5x))=x+5cos5x
d/dx(sinx5x)=(dcosu)/du * du/dx
u=5x
d/du(cosu)=cosu
d. 1/√(1-3x)+6x=d/dx(1/√(1-3x))+6*d/dx(x)=6*d/dx(x)-(d/dx(1-3x)/(2(1-3x)^(3/2))=6*d/dx(x)-d/dx(1)-3*d/dx(x)*1/(2(1-3x)^(3/2))=6*d/dx(x)+3/(2(1-3x)^(3/2))=6+3/(2(1-3x)^(3/2))
d/dx(1/√(1-3x))=d/du * 1/√u * du/dx
u=1-3x
d/du(1/√u)=-1/(2u^(3/2))
2) х%= 100тг/200/100%
Х%=50%
ответ на 50