РЕШЕНИЕ
1 - построение фигуры.
Координатная плоскость - это тетрадка в "клеточку".
Известно, что размер клетки в тетради - 5 мм.
Единичный отрезок в 1 см - 2 клетки.
Координаты точек записываются в виде: А(Ах;Ау) -
на первом месте координата по оси абсцисс - оси Х - горизонтальной оси;
на втором месте координата по оси ординат - оси У - вертикальной оси.
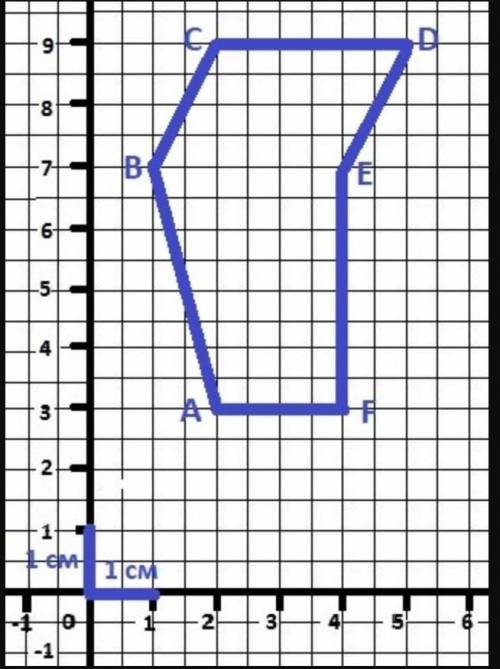
Построение фигуры по координатам данных точек - на рисунке 1 в приложении.
2 - вычисление площади фигуры.
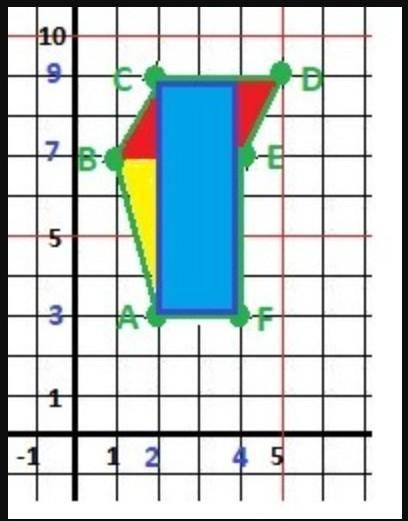
Многоугольную фигуру ABCDEFA можно разбить на простые фигуры для которых известны формулы площади.
Рисунок 2 к задаче - в приложении.
Получаем один прямоугольник (голубой) площадь которого по формуле
S1 = a*b = (9-3)*(4-2) = 6*2 = 12 см².
Площадь треугольников по формуле S = a*b/2.
Два треугольника (красных)
S2 = S3 = 1/2*1*2 = 1 см² и
один треугольник (жёлтый)
S4 = 1/2*4*1 = 2 см²
Находим площадь фигуры сложением площадей отдельных фигур.
S = 12 + 2*1 + 2 = 16 см² - площадь - ОТВЕТ
ну както так
Пошаговое объяснение:
В 235 году до н.э. греческий ученый Эратосфен изобрел следующий нахождения простых чисел на промежутке от 1 до заданного N:
1. Выписать все целые числа 2,...,N.
2. Зачеркнуть все числа, кратные i = 2 — первому простому числу.
3. Найти первое незачёркнутое число в списке, большее чем i, и присвоить значению переменной i это число.
4. Повторять шаги 2 и 3, пока это возможно.
После завершения алгоритма незачеркнутыми останутся все простые числа, меньшие либо равные N.
Напишите функцию eratosthenes(N), воспроизводящую данный алгоритм. Ваша функция должна через пробел печатать числа в том порядке, в котором их вычеркивает из списка оригинальный алгоритм. Например, если N = 10, то числа будут вычеркиваться в таком порядке: 4 6 8 10 9.
Если для какого-то параметра никакие числа не вычеркиваются, просто не выводите ничего.
ответ: