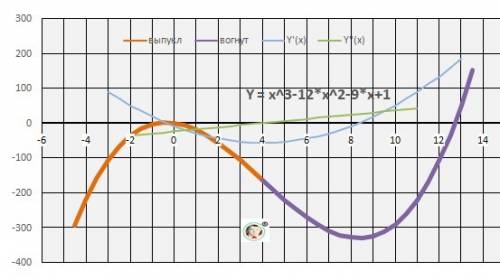
Дано: y = x³ - 12*x² - 9*x + 1
ИССЛЕДОВАНИЕ.
1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ. Y(x)=0.
x1*х2*х*х3 = 1
Разложим многочлен на множители. Y=(x-(-0,8)*(x-0,1)*(x-12,7)
Нули функции: Х₁ = -0,8, Х₂ =0,1, Х₃ =12,7
3. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X=(-oo;-0,8]U[0,1;12,7]
Положительная -Y(x)>0 X=[-0,8;0,1]U[12,7;+oo)
4. Пересечение с осью OY. Y(0) = 1
5. Исследование на чётность.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 3*x² -24*x - 9 = 0.
Корни при Х₄= =0.36, Х₅ = 8.36
Схема знаков производной - положительная парабола - отрицательная между корнями.. (-∞)__(>0)__(Х₄)___(<0)___(Х₅)__(>0)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(-0.36)= 2.6 , минимум – Ymin(8.36) = - 328,6.
8. Интервалы возрастания и убывания.
Возрастает Х=(-оо;-0,36;]U[8,36;+oo) , убывает - Х=[-0,36;8,36] 9. Вторая производная - Y"(x) = 6*x - 24=0.
Корень производной - точка перегиба Х₆= 4.
10. Выпуклая “горка» Х∈(-∞; 4).
Вогнутая – «ложка» Х∈[4; +∞).
11. Область значений: Е(y) = R, У = {-oo;+oo}
12. Таблица, график и шаблон исследования в приложении.


Чтобы сложить (вычесть) десятичные дроби, нужно:
уравнять в этих дробях количество знаков после запятой; записать их друг под другом так, чтобы запятая была записана под запятой; выполнить сложение (вычитание), не обращая внимания на запятую; поставитьв ответе запятую под запятой в данных дробях.
Число 0,444 можно записать в виде суммы:
0,444 = 0,400 + 0,040 + 0,004 = 0,4 + 0,04 + 0,004.
Оно равно сумме 4 десятых, 4 сотых и 4 тысячных.
Таким образом, в записи этого числа первая цифра 4 показывает число десятых, вторая — число сотых, а третья — число тысячных. Поэтому первый разряд после запятой называют разрядом десятых, второй — разрядом сотых, а третий — разрядом тысячных.
Запись 0,444 = 0,4 4- 0,04 + 0,004 называют разложением числа 0,444 по разрядам.