ДАНО: Y = x² - 4, Y = x - 2
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
Площадь фигуры - интеграл разности функций.
1. Находим пределы интегрирования - находим точки пересечения.
У1 =х² - 4 = У2 = х - 2
х² - х - 2 = 0 - решаем квадратное уравнение - это и есть разность функций.
b = - 1 - нижний предел, a = 2 - верхний предел.
2, Записываем разность функций - в обратном порядке и интегрируем.
s(x) = 2 - x - x² - интегрируем - находим первообразную.
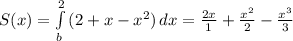
Лично мне нравится такая запись интеграла - понятно как получаются коэффициенты.
3. Вычисляем значения подставив пределы интегрирования.
S(2) = 4 +2 - 2 2/3 = 3 1/3 - подставили верхний предел
S(-1) = - 2 + 1/2 - 1/3 = - 1 1/6 - подставили нижний предел
S = S(2) - S(-1) = 3 1/3 - 1 1/6 = 4 1/2 = 4.5 - площадь - ОТВЕТ
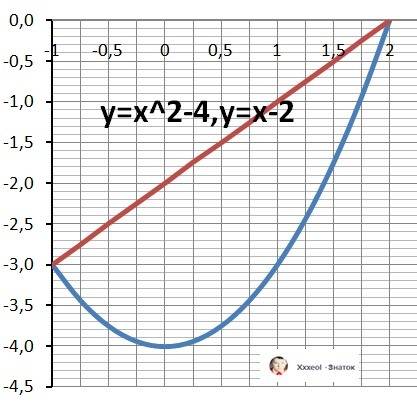
Рисунок к задаче в приложении.
Для решения применим формулу, которая связывает видимую звездную величину m с абсолютной звездной величиной М
М = m + 5 - 5lg D,
где D - расстояние от звезды до Земли в парсеках, D = 8,1 пк;
m - звездная величина, m = 0,14
М- звездная величина, которую наблюдали бы с расстояния данной звезды со стандартного расстояния 10 парсек.
М = 0,14 + 5 - 5lg 8,1 = 0,14 + 5 - 5*0,9 = 0,6
Абсолютная звездная величина связана со светимостью L формулой
lg L = 0,4 (5 - М);
lg L = 0,4 (5 - 0,6) = 1,76;
L = 58
ответ: в 58 раз ярче Солнца