 .На прямой отложим от выбранной точки
.На прямой отложим от выбранной точки  отрезок, равный данному зелёному отрезку, и обозначим его конец точкой
отрезок, равный данному зелёному отрезку, и обозначим его конец точкой 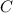 .Берём циркуль и проводим окружность с центром в точке
.Берём циркуль и проводим окружность с центром в точке  и радиусом, который равен длине жёлтого отрезка.Снова берём циркуль и проводим окружность с центром в точке
и радиусом, который равен длине жёлтого отрезка.Снова берём циркуль и проводим окружность с центром в точке 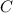 и радиусом, который равен длине фиолетового отрезка.Точка пересечения окружностей - 3 вершина треугольника.
и радиусом, который равен длине фиолетового отрезка.Точка пересечения окружностей - 3 вершина треугольника.
Построй квадрат, периметр которого равен 24 см. Вычисли площадь этого квадрата. Какими могут быть длина и ширина прямоугольника с такой же площадью?
Формула периметра квадрата:
P = 4a , где а - сторона квадрата.
Тогда:
4a = 24
a = 24 : 4
a = 6 (см)
Формула площади квадрата:
S = a²
S = 6² = 36 (см²)
Формула площади прямоугольника:
S = a * b, где а и b не параллельные стороны фигуры.
Найдем все целочисленные значения а и b, при которых площадь будет равна 36 см² методов подбора:
1 см и 36 см
2 см и 18 см
3 см и 12 см
4 см и 9 см
9 см и 4 см
12 см и 3 см
18 см и 2 см
36 см и 1 см
Алгоритм
1) Строим произвольный луч в точке A
2) На построенном луче от его начала отложим отрезок равный 4 см. Не меняя раствор циркуля проводим дугу окружности с центром в точке A, чтобы дуга пересекла луч. Точку называем C
3) Замеряем циркулем отрезок равный 3 см
4) Построим дугу окружности с центром в точке A, не меняя раствор циркуля
5) Замеряем отрезок равный 2 см
6) Не меняя раствор циркуля строим дугу окружности с центром в точке С, так чтобы эта дуга пересекалось со 2 дугой. Называем точку B
7) Соединяем точки и получаем треугольник ABC