Пусть мальчики и девочки образуют многоугольник (2-регулярный граф). Ребро, соединяющее две вершины, покрасим в черный, если две вершины одного пола, и белым в обратном случае. Пусть девочка закодирована числом 0, а мальчик — 1.
Нетрудно видеть, что граф разделился на чередующиеся островки белого и черного. На концах черных островков стоят одинаковые числа. Сумма концов черных островков четна. Поэтому сумма концов белых островков тоже четна. Рассмотрим два вида белых островков — те, что содержат четное количество ребер, и те, что содержат нечетное их количество. Нечетные белые островки имеют начало и конец в разных цифрах, а поскольку сумма цифр четна, то нечетных белых островков четное количество.
Пусть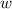 
— суммарное количество белых островков, а 
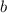— суммарное количество черных. По условию 
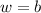, значит, 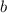четно. Всего 
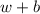ребер, что равно 
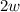— делится на 4. Количество ребер совпадает с количеством детей.
у=х³-3х²+2
находим производную и приравниваем её к нулю:
у`=3х²-6х=3х(х-2)
у`=3х²-6х=3х(х-2)у`=0
у`=3х²-6х=3х(х-2)у`=03х(х-2)=0
у`=3х²-6х=3х(х-2)у`=03х(х-2)=0х=0 та х=2
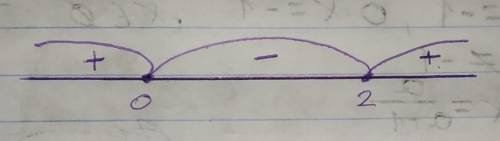
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -1, тогда производная будет равна 9, для второго возьмём 1, тогда производная будет -3 , а для третьего возьмём 3, тогда производная будет 9. Проставляем соответствующие знаки(см.рис)
Видим, что при прохождении через точку 0 производная меняет знак с плюса на минус, то есть это будет точка максимума, а при прохождении через 2 – с минуса на плюс, соответственно это точка минимума.
ОТВЕТ: 0
2) 8 : 2/3 = 8 * 3/2 =8 * 12/1 = 96
3) 8 : 2/8 = 8 * 8/2 = 8 * 32/1 = 256