Длина огорода 80 метров, а ширина 32 метра. три восьмых огорода занята картошкой, а остальная часть - id760111120200407 от kama1ezeGggggg 07.04.2020 05:09

Question

Математика: Длина огорода 80 метров, а ширина 32 метра. три восьмых огорода занята картошкой, а остальная часть морковью. сколько квадратных метров занято морковью? (сделать с пояснением)

kama1ezeGggggg · Accepted Answer

Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -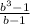 $\frac{b^{3} - 1}{b - 1}$ · X
После четвертой выплаты сумма оставшегося долга равна:
S4 = 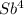$Sb^{4}$ - (1 + b +b² + b³)X = 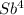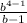$Sb^{4}$ - $\frac{ b^{4 - 1} }{b - 1}$ · X
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому 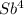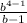$Sb^{4}$ - $\frac{ b^{4 - 1} }{b - 1}$ · X = 0.
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X = $\frac{6902000 * 1,601806640625 * 0,125 }{0,601806640625} = 2296350$ рублей

MOGZ ответил