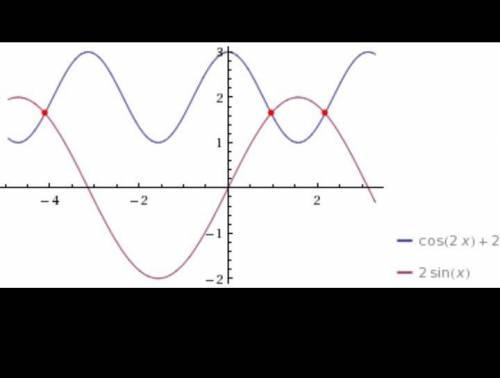
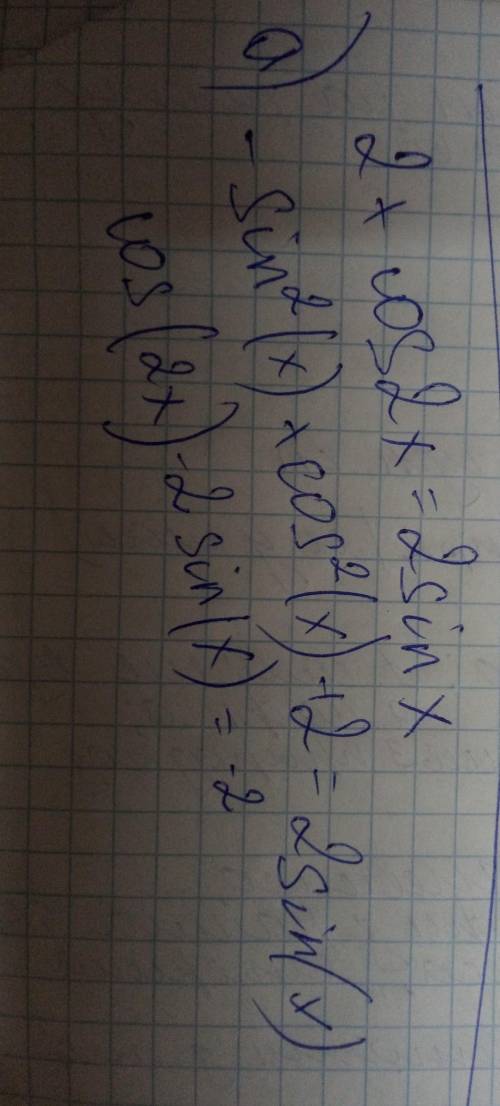Вообще, как составить функцию, обратную данной?
Любая функция записывается с букв "у" и "х"
"у" - это функция, "х" - это аргумент. Так вот. Надо найти х(у) . Она и будет обратной по отношению к данной.
Смотрим.
1) у = 0,5х +3
0,5х = у -3
х = 2у -6
Только в ответ запишем у = 2х -6 (чтобы "у" было функцией, "х" - аргументом. )
2) у = 2/(х -3)
у(х -3) = 2
ух -3у = 2
ух = 2 +3у
х =(2+3у)/у
Только в ответ запишем у =(2+3х)/х (чтобы "у" было функцией, "х" - аргументом. )
3) у = (х +2)³
х +2 = ∛у
х = -2 + ∛у
Только в ответ запишем у = -2 + ∛х
4) у = х³ -1
х³ = у +1
х = ∛(у +1)
Только в ответ запишем у = ∛(х +1)
b)
3-3cosx=2(< var > 2cos^{2}(x) < /var ><var>2cos
2
(x)</var> -1)
4< var > cos^{2}(x)+3*cos(x)-5=0 < /var ><var>cos
2
(x)+3∗cos(x)−5=0</var> cos(x)=t,-1<t<1
4t^2+3t-5=0
D=9+80=89
< var > \sqrt{D}=89\approx=9.4 < /var ><var>
D
=89≈=9.4</var>
< var > x_1=(-3-9.4)/8=-5/8 < /var ><var>x
1
=(−3−9.4)/8=−5/8</var>
< var > x_2=(-3+9,4)/8=0.8 < /var ><var>x
2
=(−3+9,4)/8=0.8</var>
Обратная замена
cosx=-5/8 cosx=0.8
x=+-arccos(-5/8)+2< var > \pi < /var ><var>π</var> *n x=+-arccos(0.8)+2< var > \pi < /var ><var>π</var> *n