ответ:
если х рабочих, делают работу (условно назовём ее объем 1) за у дней, можно записать первое уравнение ху=1,
(х-3) рабочих за (у+6) дней, то второе уравнение будет (х-3)(у+6)=1
(х+2) рабочих за (у-2) дней, составим третье уравнение - (х+2)(у-2)=1, решаем получившуюся систему из трёх уравнений: ху=ху-3у+6х-18=ху+2у-4-2х; преобразуем в два уравнения: 6х-3у-18=0 и 2у-2х-4=0; у=(6х-18)/3 и у=(2х+4)/2, х=8, у=10. нужно 8 рабочих, которые выполнят ее за 10 дней. если 5 рабочих, то за 16 дней, если 10 рабочих, то за 8 дней.
ДАНО
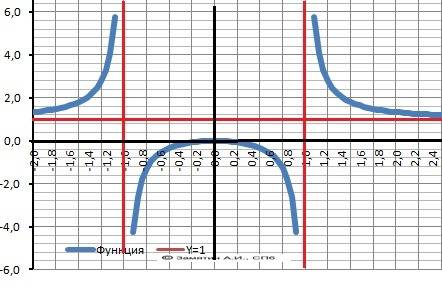
Y=x²/(x²-1)
ИССЛЕДОВАНИЕ
1.Область определения D(x)
(x²+1) =(x-1)(x+1)≠0.
Х∈(-∞;-1)∪(-1;1)∪(1;+∞0. Разрыв функции при Х = +/-1.
Вертикальные асимптоты - Х= -1 и Х=1.
2. Пересечение с осью Х. Y=0 при х = 0.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.
lim(-∞) У(х/х) = +1 limY(+∞) =+1.
5. Исследование на чётность.Y(-x) = Y(x).
Функция чётная.
6. Производная функции -Y'(x)
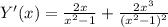
7. Локальные экстремумы. Максимум Ymax(0)= 0
8. Интервалы возрастания и убывания.
Возрастает - Х∈(-∞;-1)∪(-1;0) , убывает = Х∈(0;1)∪ (1;+∞).
8. Вторая производная - Y"(x) = ?
Корень производной - нет.
Выпуклая “горка» Х∈(-1;1), Вогнутая – «ложка» Х∈(-∞;-1)∪(1;+∞).
11. Наклонная асимптота - совпадает с горизонтальной - Y = 1.
12. График в приложении.