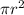 , можно найти
, можно найти 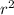 =9 => r=3. Если у нас один из катетов равен 3, а гипотенуза равна 5, то, вспоминая египетский треугольник, можно узнать величину другого катета - 4. Это и есть x, но это только половина высоты => вся высота равна 8. Зная площадь основания и высоту, можно найти V=S*h=9
=9 => r=3. Если у нас один из катетов равен 3, а гипотенуза равна 5, то, вспоминая египетский треугольник, можно узнать величину другого катета - 4. Это и есть x, но это только половина высоты => вся высота равна 8. Зная площадь основания и высоту, можно найти V=S*h=9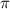 *8=9*3*8=216.
*8=9*3*8=216.
вроде как-то так)
пусть скорость пешехода х км/ч, тогда скорость велосипедиста 3,4х км/ч. Скорость приближения велосипедиста (3,4х - х) км/ч. По условию задачи с этой скоростью велосипедист догонял пешехода 0,25 часа и проехал 2,1 км. Составляем уравнение:
(3,4х-х)*0,25=2,1
2,4х*0,25=2,1
0,6х=2,1
х=3,5 (км/ч) -скорость пешехода
скорость велосипедиста 3,4х =3,4*3,5 = 11,9 км/ч
ответ:3,5км/ч;11,9 км/ч.