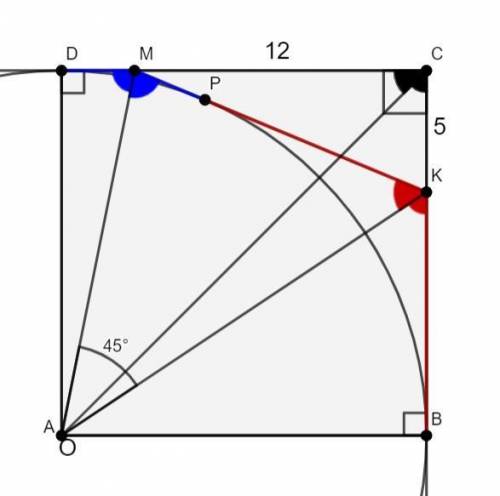
Определим центр вневписанной окружности ΔCMK, которая касается MK. Центр вневписанной окружности в треугольник лежит на пересечении биссектрисы внутреннего угла, противолежащего стороне касания, и биссектрис двух внешних углов, прилежащих к стороне касания.
Пусть центр это т. О, тогда KO - биссектриса ∠BKM; BO - биссектриса ∠DMK; OC - биссектриса ∠BCM.
Сумма внутренних углов треугольника равна 180°.В ΔMKO:
∠MOK = 180°-(∠OMK+∠OKM)
Биссектриса делит угол пополам.∠MOK = 180°-(∠DMK:2 + ∠BKM:2);
∠MOK = 180°-(∠DMK+∠BKM):2.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.Для ΔCMK:
∠BKM = ∠KMC+∠KCM;
∠DMK = ∠MKC+∠MCK.
Тогда получим:
∠MOK = 180°-(∠MKC+∠MCK + ∠KMC+∠KCM):2;
∠MOK = 180°-(180°+90°):2;
∠MOK = 180°-270°:2 = 180°-135°;
∠MOK = 45°.
Диагонали квадрата делят угол пополам.Для квадрата ABCD:
CA - биссектриса ∠BCD.
Заметим, что ∠MAK = 45° = ∠MOK и CA совпадает с CO, тогда т. А совпадает с т. О.
По определению вневписанная окружность касается продолжений CM и CK. Тогда радиус равен расстоянию от A до CM, то есть стороне квадрата. Значит окружность содержит точки D и B. CD и CB - касательные к вневписанной окружности.
Пусть P точка касания со стороной MK.
Отрезки касательных проведённых из одной точки к одной окружности равны.Поэтому MD=MP и KP=KB.
PΔCMK = CM+MK+CK;
CM+MP+PK+CK = 12+13+5;
CM+BD+CK+KM = 30;
2·CD = 30;
CD = 30:2 = 15.
ответ: 15.