Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: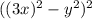 
; В следующих двух слагаемых вынесем общий множитель "40": 
; В итоге получим следующее уравнение: 
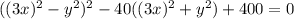. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо 
будет стоять 
; Это приведет к тому, что придется убавить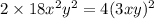 
; В итоге: 
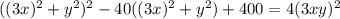; Слева стоит квадрат суммы. Уравнение примет вид: 
; Сворачивая еще раз: 
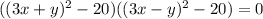; Получаем серию прямых: 
; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом 
; Рассмотрим прямую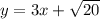 
; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 
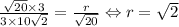; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 
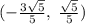; Ну а все решения:
Названия созвездиям придумали еще в древнем мире. Людижили преимущественно в северном полушарии Земли и виделитолько открытую им часть небесной сферы. Поэтому примернополовина (47 из 88) созвездий издавна названа в честь мифо-логических персонажей. Другая часть - видимая из южногополушария - была открыта и получила названия в XVII веке,после Великих географических открытий.Покажи на числовом промежутке луча множество решенийдвойного неравенства 47 < x < 88 и назови числа. Сколькочисел получилось? Сколько созвездий получили названияв XVII веке?
Пошаговое объяснение:
3000 г :100*6=180 г
3000:100*29=870(р.) - на столько подешевел прибор