В прямоугольном треугольнике АВН определим величину угла АВН. Угол АВН = 180 – АНВ – ВАН = 180 – 90 – 60 = 300. Тогда катет АН лежит против угла 300 и равен половине длины гипотенузы АВ. АН = 8 / 2 = 4 см.
Тогда ВН2 = АВ2 – АН2 = 64 – 16 = 48.
ВН = 4 * √3 см.
По условию, ВН делит АД пополам, тогда АН = ДН = 4 см.
АД = АН + ДН = 4 + 4 = 8 см.
ВСДН – прямоугольник, так как ВН высота, а СДА = 900 по условию, тогда СВ = ДН = 4 см.
Определим площадь трапеции.
Sавсд = (СВ + АД) * ВН / 2 = (4 + 8) * 4 * √3 / 2 = 24 * √3 см2.
ответ: Площадь трапеции равна 24 * √3 см2.
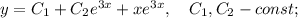
Пошаговое объяснение:
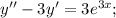
Это неоднородное уравнение. Сначала решим соответствующее ему однородное уравнение:
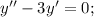
Составим и решим характеристическое уравнение:
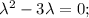
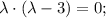

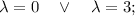
Имеем 2 различных действительных корня. Запишем общее решение однородного уравнения:
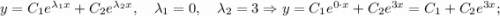
Вернёмся к неоднородному уравнению.
Показатель степени экспоненты содержит коэффициент, равный одному из корней характеристического уравнения, поэтому частное решение будем искать в виде
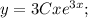
Найдём первую и вторую производные:
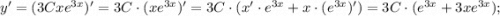
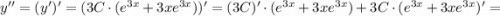
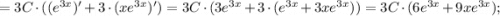
Подставим полученные производные в исходное уравнение:
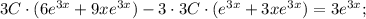
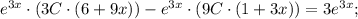
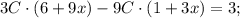
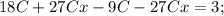
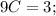
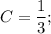
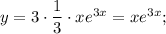
Проверим, верно ли найдено частное решение неоднородного уравнения. Воспользуемся ранее найденными производными:
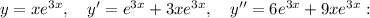
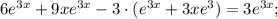
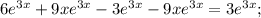
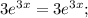
Частное решение найдено верно.
Общим решением неоднородного дифференциального уравнения является сумма общего решения однородного ДУ и частного решения неоднородного ДУ:
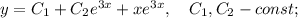
2) 2430-1120=1310(кг)-масса сазана
3) 2430-1600=830(кг)-масса леща
4) 830+1310=2140(кг)-масса сазана и леща
5) 2430-2140=290(кг)-масса окуня