1. Розкриємо тангенс суми кутів для правої та лівої частини рівняння
2. Скористаємося формулою тангенсу суми кутів для зведення сум кутів у правій частині до однакового вигляду:
3. Віднімемо від обох частин рівняння tg(3x), щоб звести його до вигляду tg(7x) = tg(2x)
4. Розв'яжемо рівняння tg(7x) = tg(2x) для знаходження значень x
Отже, загальний розв'язок рівняння tg(x) + tg(4x) = tg(2x) + tg(3x) має вигляд x = kπ/5, де k - ціле число.
Пошаговое объяснение:
На фото, у відповіді просто пояснення кроків розв'язку цього рівняння.
Будь ласка, відміть цю відповідь як найкращю
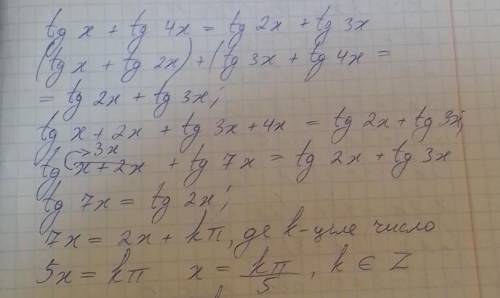
2)38 400:12 800=3(шоколадки)
1)40 500:3=13 500(Цена за 1/4 кг конфет)
2)13 500×4=54 000(Цена за 4/4 кг(1кг) конфет )