Во-первых, специальным образом пронумеруем монеты: присвоим им трехзначные номера 001, 010, 011, 012, 112, 120, 121, 122, 200, 201, 202, 220.
Для первого взвешивания положим на одну чашу весов те монеты, у которых старший разряд равен 0 (то есть 001, 010, 011, 012), а на другую - те монеты, у которых он равен 2 (200, 201, 202, 220). Если перетянет чашка с ``0'', запишем на бумажке цифру 0. Если перетянет ``2'' — запишем 2. Если чаши весов останутся в равновесии — запишем 1.
Для второго взвешивания на одну чашу выложим монеты 001, 200, 201, 202 (то есть все те монеты, у которых второй разряд равен 0), а на другую — 120, 121, 122, 220 (то есть те монеты, у которых средний разряд равен 2). Запишем результат взвешивания таким же образом, что и при первом взвешивании.
Третьим взвешиванием сравниваем 010, 020, 200, 220 с 012, 112, 122, 202 (соответственно, нули и двойки в младшем разряде) и записываем третью цифру.
Мы получили три цифры — иначе говоря, трехзначное число. Далее определяем фальшивую монету по следующему рецепту:
Если это число совпадает с номером какой-то монеты, то эта монета фальшивая и тяжелее остальных. Если нет, то заменим в этом числе все нули на двойки, а все двойки на нули. После этого оно должно совпасть с номером какой-то монеты. Эта монета фальшивая и легче остальных.
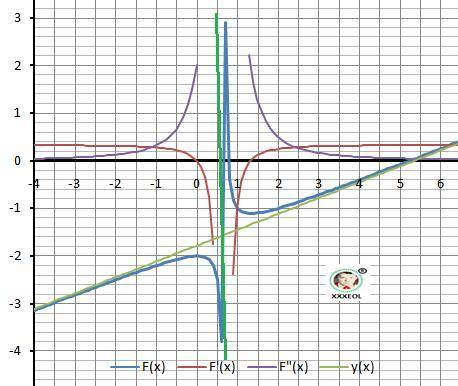
Дано: y = (x²-6x+4)/(3x-2),
ИССЛЕДОВАНИЕ.
1. Область определения: D(y)= X≠ 2/3 , X∈(-∞;2/3)∪(2/3;+∞). Не допускаем деления на 0 в знаменателе.
2. Разрыв II-го рода при Х = 1. Вертикальных асимптота - Х = 2/3.
3. Наклонная асимптота: k = lim(+∞)Y(x0/x = 1/3
b = -16/9 и
y(x) = x -16/9 - наклонная асимптота.
4. Нули функции, пересечение с осью ОУ.
y(0) = 4 : (-2) = -2
Пересечение с осью ОХ - решаем квадратное уравнение в числителе.
х1 = 5,236 и х2 = 0,7639, D = 20 и √20 = 2√5
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;2/3)∪(0.76;5.2).
Положительна: Y>0 - X∈(5.2;+∞;)
6. Проверка на чётность. Есть сдвиг по оси ОХ - нет симметрии ни осевой ни центральной.
Функция общего фида - ни чётная, ни нечётная: Y(-x) ≠ -Y(x) ,
Y(-x)= (x^2+6*x+4)/(-3*x+2).
7. Поиск экстремумов по первой производной.
y'(x) =(-3*x² +18*x +2*(x-3)(3x-2)-12 /(3x-2)² = 0.
x*(3*x-4) =0
x1 = 0, x2 = 4/3 - точки экстремумов.
8. Локальный максимум: y(0) = -2, минимум: y(4/3) = -1.11.
9. Интервалы монотонности.
Возрастает - X∈(-∞;0)∪(4/3;+∞). Убывает: X∈(0;2/3)∪(3/2;4/3).
10. Поиск перегибов по второй производной.
y"(x) = 8/(3x-2)³ = 0
Точки перегиба нет, кроме разрыва при Х = 0.
11. Вогнутая - "ложка"- X∈(2/3;+∞;), выпуклая - "горка" - X∈(-∞;2/3);
12. Область значений. E(y) - y∈(-∞;+∞).
13. График функции на рисунке в приложении.