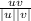
Приведу редко используемый в этой ситуации в надежде. что кто-нибудь другой даст и один из стандартных . 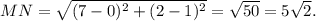
Пусть K - точка касания одной из двух касательных с окружностью. Тогда KN=\sqrt{10} - ведь уравнение окружности x²+(y-1)^2=10, центр у нее в точке N(0;1), а радиус равен корню из 10.
Далее, поскольку касательная перпендикулярна радиусу, проведенному в точку касания, угол MKN прямой, KM²=50-10=40, а тангенс угла KMN равен 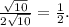
Поэтому. чтобы получить касательную, нужно прямую MN с угловым коэффициентом (то есть тангенсом угла наклона) 1/7 повернуть вокруг точки M на угол arctg(1/2) в ту или другую сторону. Поскольку
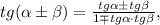 получаем угловые коэффициенты
получаем угловые коэффициенты
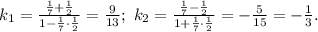
Поэтому уравнения касательных -
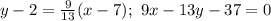 и
и
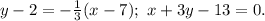
х жуков
8-х пауков
6х лап у всех жуков
8(8-х) лап у всех пауков
6х+8(8-х)=54
6х+64-8х=54
6х-8х=54-64
-2х=-10
х=5 жуков
8-5=3 паука