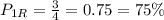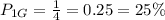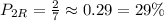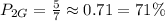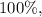Математика: Разбор слово по составу налим заранее

Разбор слово по составу налим заранее

👇

Увидеть ответ

Ответ:

nastyakolomiec1

13.01.2021

Корень - налим, окончание нулевое

4,6(69 оценок)

Открыть все ответы

Ответ:

alenaalefirova

13.01.2021

В первом случае:

вероятность достать красный шар $P_{1R} = \frac{3}{4} = 0.75 = 75 \%$ ;

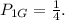вероятность достать зелёный шар $P_{1G} = \frac{1}{4} = 0.25 = 25 \%$ ;

Во втором случае:

вероятность достать красный шар $P_{2R} = \frac{2}{7} \approx 0.29 = 29 \%$ ;

вероятность достать зелёный шар $P_{2G} = \frac{5}{7} \approx 0.71 = 71 \%$ ;

О Д Н А . и н т е р п р е т а ц и я . в о п р о с а

Если тот, кто будет предсказывать цвет доставаемого шара, будет проинформирован о составе корзины, то максимально точно предсказать он сможет в том случае, если будет ВСЁ время говорить – "красный!", вообще не пытаясь угадать "зелёный!" (если при этом шар после доставания кладётся обратно). 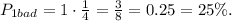При этом предсказание будет плохим, когда, например, предсказывают красный с долей $100 \% ,$ а достают зелёный с долей $P_{1G} = \frac{1}{4} .$ Общая вероятность плохого предсказания составит тут $P_{1bad} = 1 \cdot \frac{1}{4} = \frac{3}{8} = 0.25 = 25 \% .$

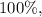Если тот, кто будет предсказывать цвет доставаемого шара, будет проинформирован о составе второй корзины, то максимально точно предсказать он сможет в том случае, если будет ВСЁ время говорить – "зелёный!", вообще не пытаясь угадать "красный!" (если при этом шар после доставания кладётся обратно). 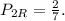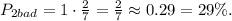При этом предсказание будет плохим, когда, например, предсказывают зелёный с долей $100 \% ,$ а достают красный с долей $P_{2R} = \frac{2}{7} .$ Общая вероятность плохого предсказания составит тут $P_{2bad} = 1 \cdot \frac{2}{7} = \frac{2}{7} \approx 0.29 = 29 \% .$

Д Р У Г А Я . и н т е р п р е т а ц и я . в о п р о с а

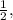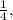Если тот, кто будет предсказывать цвет доставаемого шара, не проинформирован о составе корзины, то лучшая стратегия угадать – будет говорить в половине случаев "красный!", и в половине случаев – "зелёный!" (если при этом шар после доставания кладётся обратно). При этом предсказание будет плохим, когда, например, предсказывают красный с долей $\frac{1}{2} ,$ а достают зелёный с долей $\frac{1}{4} ,$ или наоборот, предсказывают зелёный с долей 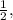$\frac{1}{2} ,$ а достают красный с долей 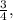$\frac{3}{4} ,$ Общая вероятность плохого предсказания составит тут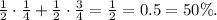 $\frac{1}{2} \cdot \frac{1}{4} + \frac{1}{2} \cdot \frac{3}{4} = \frac{1}{2} = 0.5 = 50 \% .$

Аналогично можно показать, что и для второй корзины вероятность плохого угадывания будет составлять $50 \% .$

Так что в такой интерпретации вопроса, задача не имеет чёткого ответа.

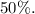
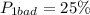О т в е т : в случае, когда угадывающий знает, какого цвета шаров в корзине больше, и начинает при угадывании всё время говорить именно преобладающий цвет, он будет делать $P_{1bad} = 25 \%$ ошибок в первом случае, и 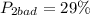$P_{2bad} = 29 \%$ ошибок во втором случае, поэтому угадывание цвета доставаемого шара менее предсказуемо во втором случае.

4,6(19 оценок)

Ответ:

Efimenko34

13.01.2021

Пусть скорость автомобиля x км/ч, тогда скорость мотоцикла x + 70 км/ч.
Через два часа автомобиль проедет 2x км, а мотоцикл — 2x + 140 км.
Согласно условию, траектории их движения перпендикулярны, значит расстояние между ними можно найти по теореме Пифагора.
(2x)² + (2x + 140)² = 260²
4x² + 4(x + 70)² = 4 · 130²
x² + (x + 70)² = 130²
x² + x² + 140x + 4900 = 16900
2x² + 140x - 12000 = 0
x² + 70x - 6000 = 0
D/4 = 35² + 6000 = 7225 = 85²
x₁ = -35 + 85 = 50
x₂ = -35 - 85 = -155 → модуль скорости не может быть отрицательным
Значит скорость автомобиля 50 км/ч, а скорость мотоциклиста 50 + 70 = 120 км/ч.
ответ: 50 км/ч, 120 км/ч

4,5(33 оценок)

Это интересно:

Образование-и-коммуникации

13.09.2022

Как легко и быстро спрягать испанский глагол hacer...

Стиль-и-уход-за-собой

03.11.2020

Описание людей: как правильно выбрать слова...

Компьютеры-и-электроника

15.02.2020

Как нарисовать шар в GIMP?...

Образование-и-коммуникации