ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
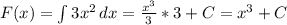
Подставляем в первообразную границы интегрирования:

2.
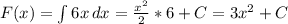
Подставляем в первообразную границы интегрирования:
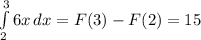
3.

Подставляем в первообразную границы интегрирования:
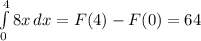
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
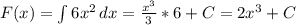
Подставляем в первообразную границы интегрирования:
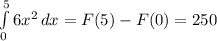
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
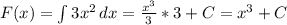
Подставляем в первообразную границы интегрирования:

2.
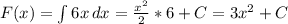
Подставляем в первообразную границы интегрирования:
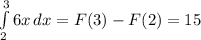
3.

Подставляем в первообразную границы интегрирования:
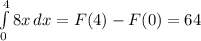
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
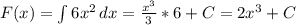
Подставляем в первообразную границы интегрирования:
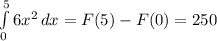
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

Центральный угол равен градусной мере дуги, на которую опирается.
∠BOC=90° (дуга BC =90°)
△BOC - прямоугольный треугольник.
По теореме Пифагора:
BC^2= BO^2 + OC^2 = 2*81 =162 (см)
Сечение цилиндра плосостью, параллельной его оси, есть прямоугольник.
∠ABC=90°
△ABC - прямоугольный треугольник.
По теореме Пифагора:
AB= √(AC^2 - BC^2) = √(225-162) = √63 =3√7 (см)
AB - образующая цилиндра (соединяет окружности оснований, параллельна оси вращения).
Все образующие имеют одинаковую длину, равную высоте цилиндра.
h=3√7 (см)