![\int \frac{\sqrt{x^2+4}}{x^4} \, dx= [\; x=2tgt\; ,\; x^2+4=4tg^2t+4=4(tg^2t+1)=\frac{4}{cos^2t}\; ,\\\\dx=\frac{2}{cos^2t}\, dt\; ,\; \frac{x}{2}=tgt\; ,\; t=arctg\frac{x}{2}\; ]=](/tpl/images/0771/4775/06e54.png)
![\int \frac{\sqrt{\frac{4}{cos^2t}}}{2^4\, tg^4t} \cdot \frac{2\, dt}{cos^2t} =\frac{1}{2^2}\int \frac{dt}{tg^4t\cdot cos^3t}=\frac{1}{4}\int \frac{cost\, dt}{sin^4t} =\\\\= \frac{1}{4}\int \frac{d(sint)}{sin^4t} = \frac{1}{4} \cdot \frac{(sint)^{-3}}{-3} +C=-\frac{1}{12sin^3t}+C=\\\\=- \frac{1}{12sin^3(arctg\frac{x}{2})} +C=[\; sin(arctg\frac{x}{2})= \frac{x}{\sqrt{4+x^2}}]](/tpl/images/0771/4775/c8d3e.png)
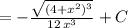
Повна площа трапеції буде 120 см² , а об"єм буде 75см³
Пошаговое объяснение:
Маємо правильну трикутню призму , тому , щоб знайти повну поверхню цієї призму , треба знайти площу основ(площа трикутника ), потім знайти площу трьох бокових сторін(прямокутники), почнемо: S осн.=АС*1/2 h, де h-висота основи h²=AB²-АК²=6²-3²=√25=5
S осн.=1/2*6*5=15 , дві основи=15*2=30см² , тепер знайдемо площу бокових сторін:3*(6*5)=90 см² Повна поверхня буде :Sосн.+S бок.=90+30=120см²
А об"єм призми буде Sосн.*H де Н висота призми, яка =5 см, тоды маємо: 15*5=75см³
29) 192
38) 6
Пошаговое объяснение:
29) Для арифметической прогрессии справедливо соотношение
Сумма членов с номерами 1 и n, равна сумме членов с номерами 2 и (n-1), равна сумме членов с номерами 3 и (n-2) и т.д. То есть если сумма номеров членов последовательности равна n+1, то равны и их суммы.
Ряд составленный из членов с номерами 3,6,9,...,3n это тоже арифметическая прогрессия значит равны суммы членов с такими номерами:
3 и 3n;6 и 3n-3;9 и 3n-612 и 3n-9То есть, если сумма номеров членов последовательности равна 3n+3, то равны и их суммы. А сумма всех членов последовательности от 3 до 3n с шагом 3 равна сумме первого и последнего, т.е n и 3n умноженное на количество таких пар, а оно равно n/2
Складываем 2n+1 и n+2, эта сумма равна 3n+3
Значит a3+a6+a9+...a3n=(a[2n+1] + a[n+2])*n/2=23*n/2=736
n=736*2/23=64
А количество членов арифметической прогрессии равно 3*64=192
38) Функция 3+5x-x^2 достигает своего максимума в точке, которая является центром отрезка [x1,x2], где x1,x2 это корни квадратного уравнения 3+5x-x^2=0. По теореме Виета сумма корней приведенного квадратного уравнения равна коэффициенту перед первой степенью x со знаком минус. В нашем случае это 5, тогда функция принимает максимальное значение при x= 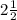 . Найдем член последовательности при n=2 он равен 9,при n=3 он тоже равен 9.
. Найдем член последовательности при n=2 он равен 9,при n=3 он тоже равен 9.
Значит значение наибольшего члена последовательности равно 9.
ответ: 15-9=6.