Построить график функции у=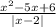
. Найти область определения функции
Пошаговое объяснение:
у=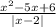 . Разложим х²-5х+6 на множители. х²-5х+6=0 ,х=2,х=3
у=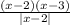
1 случай) Пусть х-2>0, х>2 , тогда |x-2|=x-2
у=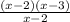
. Область определения функции х≠2 ( при х=2 знаменатель обращается в 0)
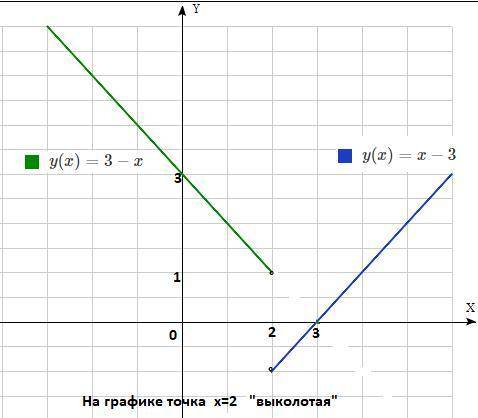
у=х-3 , х≠2. Графиком является прямая
х -2 3
у -5 0
2 случай) Пусть х-2≤0, х≤2 , тогда |x-2|= -(x-2)
у=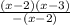
. Область определения функции х≠2 ( при х=2 знаменатель обращается в 0)
у=-(х-3) , у=3-х , х≠2. Графиком является прямая
х -2 3
у 5 0
На графике точка х=2 "выколотая"
Область значений функции (-1 ; 1)∪( 1 ;+∞)
1) Сначала разложим каждое число на множители и получим:
35 = 5 * 7 * 1;
77 = 7 * 11 * 1;
Для того, чтобы найти НОК чисел, запишем множители у большего числа и к нему добавим множители другого числа, которых нет у первого числа. Затем найдем произведение записанных множителей.
НОК (35; 77) = 7 * 11 * 5 = 77 * 5 = 385.
Для того, чтобы найти НОД чисел, запишем общие множители чисел и найдем его произведение.
НОД (35; 77) = 7 * 1 = 7.
2) 96 = 2 * 2 * 2 * 2 * 2 * 3 * 1;
26 = 2 * 13 * 1;
НОК (96; 26) = 96 * 13 = 1248.
НОД (96; 26) = 2 * 1 = 2.
3) 21 = 3 * 7 * 1;
84 = 2 * 2 * 3 * 7 * 1;
НОК (21; 84) = 84;
НОД (21; 84) = 3 * 7 * 1 = 21.
7x-9x= -3,2+1,4 -8y+1,2=1,2-4,5y+5,6
-2x= -1,8 -8y+4,5y=1,2+5,6-1,2
x=0,9. -3,5y=5,6
y= -5,6/3,5.
"y= -1,6."
2. _4x_ -2=_1_ 1)16x-56=7 2)4x-2=1 3)16x-56=1
7 4 16x=7+56 4x=3 16x=1+56
16x=63 x=3/4 16x=57
_4x_=_1_+2 x=63/16 x=0,75. x=57/16
7 4 x=3,93. x=3,56.
_4x_=_5_
7 4 4)4x-2=28
4x=28+2
x=_5_÷_4_ 4x=30
4 7 x=30/4
x=7,5.
x=_5_ ·_7_=_35_
4 4 16
x=_35_=2,18.
16