на фотографиях
Пошаговое объяснение:
10) нужно было привести q и сделать уравнение
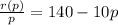
11) нужно представить рабочих в виде дроби (время)
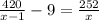 , так как первый рабочий затрачивает на 9 часов меньше, чем второй
, так как первый рабочий затрачивает на 9 часов меньше, чем второй
12) необходимо найти экстремумы функции в данном отрезке через первую производную. Так как функция представлена в виде перемножения 2 функций, то используем формулу y'=(u)'(v)'=u'v + v'u
Потом находим подходящее значение функции, которое должно находится между 5 и 14 по аргументу (x). После этого подставляем подходящее (10) в уравнение ФУНКЦИИ и находим значение y, которое равно 3. Получается что график функции будет выпуклым вниз на участке [5;14] в значении x = 10, а значении y = 3.




Пусть Р(А) - вероятность попасть в сборную
Тогда
P(B₁) = 4 / 15 - вероятность, что отберут первокурсника
P(B₂) = 2 / 5 - вероятность, что отберут второкурсника
P(B₃) = 1 / 3 - вероятность, что отберут третьекурсника
По условию задачи
P(A | B₁) = 0.9, P(A | B₂) = 0.8, P(A | B₃) = 0.7
По формуле полной вероятности
P(A) =
P(B₁) * P(A | B₁) + P(B₂) * P(A | B₂) + P(B₃) * P(A | B₃) =
0.9 * 4 / 15 + 0.8 * 2 / 5 + 0.7 * 1 / 3 =
0.24 + 0.32 + 0.23 = 0.7933
Вероятность того, что это будет второкурсник рассчитывается по формуле Байеса:
P(B₂ | A) = P(B₂) * P(A | B₂) / P(A) = 0.4 * 0.8 / 0.7933 = 0.4034
8x = p/2 + 2pn, n ∈ Z
x= p/16 + 1/4 pn, ∈ Z
sin 5x = 0
5x = pm, m ∈ Z
x= 1/5 pm, m ∈ Z
sin (2x- p/18) = -1/2
2x - p/18 = -p/6 + 2pk, k ∈ Z
2x= -2p/18 + 2pk, k ∈ Z
x= -p/36 + pk, k ∈ Z
и
2x - p/18 = -5p/6 + 2pl, l ∈ Z
2x = -13p/18 + 2pl, l ∈ Z
x= -13p/36 + pl, l ∈ Z
cos(6x+3p/10) = √3/2
6x+ 3p/10 = p/6 + 2pl, l ∈ Z
6x = -2p/15 + 2pl, l ∈ Z
x= -p/45 + 1/3 pl, l ∈ Z
и
6x + 3p/10 = -p/6 + 2pr, r ∈ Z
6x = -4p/15 + 2pr, r ∈ Z
x= - 2p/45 + 1/3 pr, r ∈ Z