Пошаговое объяснение:
Одинаковыми буквами зашифрованы одинаковые цифры, разными буквами - разные. В данной задаче используются только 6 цифр - от 0 до 5.
Какое число зашифровано за словом «ЛАЙ»?
Правильный ответ находится путем проверки каждого из знаков.
Если от числа отнять равное ему число, получим 0. Начнем решение, используя названный тезис. Л − Л = Й, значит, Й = 0. Самая большая цифра - 5. Из условия задачи известно, что У = 4, значит Е = 5, А = 1. За буквами Л и М зашифрованы оставшиеся цифры 2 и 3. М > Л. Соответственно, М = 3, а Л = 2.
352 − 142 = 210
ответ: 210.
Одинаковые цифры обозначены одинаковыми буквами, разные цифры – разными.
Какое число спряталось за словом «ДАЧА»?
При решении исходим из того, что П Ч = 5, поэтому из-за перехода через десяток А = 2, а Н = 6 и Л = 1.
Д – четное, так как нет перехода через десяток. Д ≠ 0, Д ≠ 2, Д ≠ 6.
Если предположить, что Д = 4, то П = 2 = А, а такой вариант невозможен.
Следовательно, Д = 8, а П = 4.
4126 + 4126 = 8252.
ответ: 8252.
190 прямых
Пошаговое объяснение:
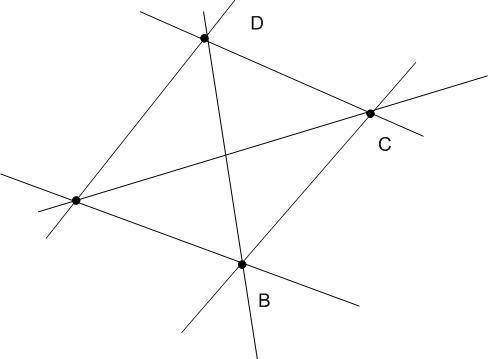
попробуем построить, ну, например для 4-х точек (см.рис).
Прямая проходит через каждые две точки. Т.е. нужно посчитать сколько различных пар точек можно выбрать из 4-х точек. Это - известная в комбинаторике формула для подсчета числа сочетаний (именно сочетаний, а не размещений, потому, что прямая АВ и прямая ВА - одна и таже прямая). Подсчитаем для 4-х точек:
C₄²=4!/(4-2)!4!=4!/(2!*2!)=3*4/2=6;
и действительно видим 6 прямых. Тогда для 20 точек:
C₂₀²=20!/((20-2)!2!)=19*20/2=190.
Как-то так)