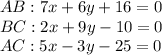
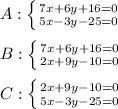
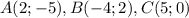
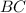 как уравнение с угловым коэффициентом:
как уравнение с угловым коэффициентом: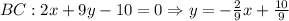
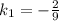
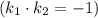 найдем
найдем 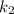 – угловой коэффициент прямой, содержащей высоту
– угловой коэффициент прямой, содержащей высоту 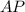 :
: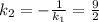
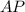 найдем по точке
найдем по точке 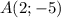 и угловому коэффициенту
и угловому коэффициенту 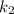 :
: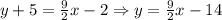
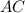 как уравнение с угловым коэффициентом:
как уравнение с угловым коэффициентом: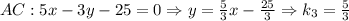
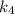 – угловой коэффициент прямой, содержащей высоту
– угловой коэффициент прямой, содержащей высоту 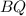 , то
, то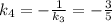
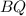 найдем по точке
найдем по точке 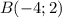 и угловому коэффициенту
и угловому коэффициенту 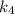 :
:
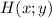 найдем, решив систему уравнений, задающих прямые
найдем, решив систему уравнений, задающих прямые 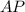 и
и 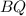 :
: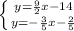
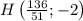
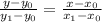
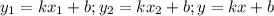
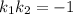 - признак перпендикулярности на плоскости
- признак перпендикулярности на плоскости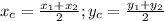
Если 14 чел = 4%, то всего студентов 14*100/4 = 14*25 = 350.
Если 14 чел = 5%, то всего студентов 14*100/5 = 14*20 = 280.
Значит, их было от 280 до 350 человек.
Причем это количество делится на 6 (шестая часть получили уд.)
и 56% от их числа есть число целое (56% получили хор.)
Такое число только одно - 300.