
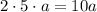
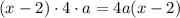
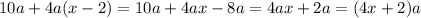
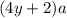 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: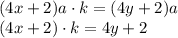
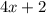 и выражение
и выражение 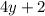 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном 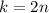 возникает противоречие:
возникает противоречие: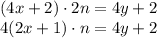
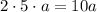
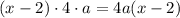
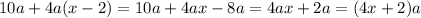
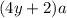 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: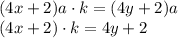
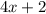 и выражение
и выражение 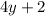 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном 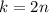 возникает противоречие:
возникает противоречие: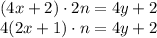
рассуждаем так: был знаменатель 9, станет - 54, во сколько раз он увеличится - 54 : 9 = 6, значит, и числитель нужно умножить на 6.
Основное свойство дроби гласит: числитель и знаменатель дроби можно умножить или разделить на одно и то же, неравное 0 число, при этом дробь останется прежней.