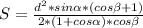 В основании данной пирамиды лежит ромб.
В основании данной пирамиды лежит ромб.
Следовательно, площадь S полной поверхности данной пирамиды равна сумме S1 –(площади основания), и S2 –(площади 4-х равных боковых сторон).
Примем сторону основания равной а.
Формула площади параллелограмма S=a•b•sinα, где a и b соседние стороны, α -угол между ними. Стороны ромба равны. Поэтому
S1=a²•sinα
S2=SH•4a:2=SH•2a (SH- высота боковой грани)
S=a²•sinα+2a•SH
Так как боковые грани наклонены к основанию под одинаковым углом, ОН=r вписанной в основание окружности, равен половине высоты h основания и по т. о трёх перпендикулярах является проекцией высоты SH боковой грани, а угол SHO= β =>
SH=OH:cosβ
OH= 0,5•h=a•sinα/2
SH=a•sinα/2cosβ
S2=[2a•(a•sinα)/2]:cosβ=a²•sinα/cosβ
S=a²•sinα+ a²•sinα/cosβ=>
S=(a²•sinα•cosβ+a²•sinα):cosβ=a²•sinα•(cosβ+1):cosβ
--------------
Выразим а² из ∆ BCD
В ∆ DCB BD=d
∠DCB=180°- ∠CDA
cos∠DCB= - cos∠CDA= -cosα
По т.косинусов BD²=CD²+BC²-2CD•CB•(-cosα )
d²=a²+a²-2a²•(-cosα )=>
а²=d²:2(1+cosа)
Подставив в S значение а², получим:
S=d²•sinα•(cosβ+1):2(1+cosα)•cosβ
D(y)∈R
y(-x)=-2/3*x³-x²+4x+1 ни четная,ни нечетная
y`=2x²-2x-4=0
x²-x-2=0
x1+x2=1 U x1*x2=-2
x1=-1 U x2=2
+ _ +
(-1)(2)
возр max убыв min возр
ymax=-2/3-1+4+1=3 1/3
ymin=16/3-4-8+1=-5 2/3
y``=4x-2=0
x=0,5 y=-1 1/6
(1/2;-1 1/6) точка перегиба