Геометрическое место точек, равноудаленных от одной точки (фокуса) и от одной прямой (директрисы) - это парабола.
Итак, мы знаем, что фокус параболы A(-2; 5), а директриса L: y + 1 = 0
Пусть текущая точка параболы имеет координаты M(x; y).
Тогда расстояние от точки М до прямой L:

Расстояние между точкой A и точкой M:
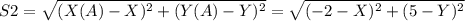
И эти расстояния одинаковы по условию:

(y+1)^2 = (x+2)^2 + (y-5)^2
(x + 2)^2 = (y + 1)^2 - (y - 5)^2 = (y + 1 - y + 5)(y + 1 + y - 5) = 6(2y - 4)
(x + 2)^2 = 12(y - 2)
Собственно, это и есть уравнение параболы в каноническом виде.
Можно перевести в более привычный для школьников вид:
12y = (x + 2)^2 + 24 = x^2 + 4x + 4 + 24
y = (x^2 + 4x + 28)/12
y = x^2/12 + x/3 + 7/3
Берем с 1 мешочка 1 монету,со 2 мешочка 2 монеты, 3 мешочка 3 монеты, с 4 мешочка 4 монеты, с 5 мешочка 5 монет и так далее до десяти мешочков.
Всего у нас получилось 55 монет(1+2+3+4+5+6+7+8+9+10=55).Кладем их на весы.Смотрим на вес:
Если фальшивая монета в 1 мешочке(у нас там 1 монета),то общий вес будет равен
1*15+54*20=1095 г
если фальшивая монеты во 2 мешочке(у нас там 2 монеты),то
2*15+53*20=1090 г
если фальшивая монета в 3 мешочке(у нас там 3 монеты),то
3*15+52*20=1085 г
И так далее до десятого мешочка.