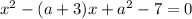
Воспользуемся теоремой Виета:
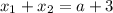
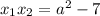
Произведение корней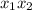 
на 2 больше суммы 
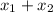этих корней, следовательно:
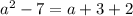
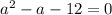
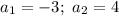
Определим, при каких значениях параметра 
данное уравнение существует.
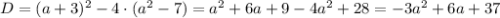
Следовательно,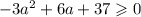 
— условие существования корней данного квадратного уравнения.
Проверим, удовлетворяют ли полученные значения параметров для решения исходного уравнения.
Если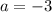 
, то получаем неправильное неравенство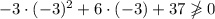 
Если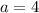 
, то получаем верное неравенство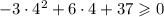 
Таким образом, только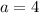 
обратит данное уравнение в таковое, что произведение корней на 2 будет больше суммы этих корней.
ответ: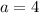
AB=5√3 см
BC=13 см
<DAB=30°
BD₁=25 см
1. ΔDAB.
теорема косинусов: DB²=AB²+AD²-2*AB*AD*cos<DAB
DB²=(5√3)²+13²-2*5√3*13*cos30°
DB²=75+169-195, DB=7 см
2. ΔBDD₁: DB=7 см, <BDD₁=90°, BD₁=25 см
теорема Пифагора: 25²=7²+DD₁²
DD₁=24 см
3. S полн. пов.=Sбок+2*Sосн
S бок=Pосн*H, S бок=2*(5√3+13)*24=240√3+624
Sосн=AB*AD*sin<DAB, S осн=5√3*13*(1/2)=32,5√3
S полн. пов=240√3+640+2*32,5√3=640+305√3
ответ: S полн.пов.=640+305√3 см²