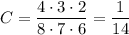
1.
Выберите правильный ответ. Какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга:
5<10 и 5>10
10>9 и 10<=9
Существуют белые слоны. Все слоны серые.
Этот треугольник равнобедренный и прямоугольный.
Этот треугольник не равнобедренный или он не прямоугольный.
Прямая а параллельна прямой b.
Прямая a перпендикулярна прямой b.
2.
Выберите правильный ответ. Ложными высказываниями являются . . .
Наличия аттестата о среднем образовании достаточно для поступления в институт
Наличие аттестата о среднем образовании необходимо для поступления в институт
Если целое число делится на 6, то оно делится на 3
Для того, чтобы четырёхугольник был квадратом, необходимо, чтобы его диагонали были равны и перпендикулярны
3.
Выберите правильный ответ. Истинными высказываниями являются . . .
Для того, чтобы четырёхугольник был квадратом, достаточно, чтобы его диагонали были равны и перпендикулярны
Наличие аттестата о среднем образовании необходимо для поступления в институт
Если целое число делится на 6, то оно делится на 3
Каждый ромб является параллелограммом
Каждый параллелограмм является ромбом
4.
Выберите правильный ответ. Объединение двух высказываний в одно с союза «и» называется…
инверсия
конъюнкция
дизъюнкция
импликация
5.
Выберите правильный ответ. Логической операцией не является…
логическое умножение
логическое деление
логическое отрицание
логическое сложение
6.
Выберите правильный ответ. Укажите логическую операцию, которая не является базовой:
конъюнкция
инверсия
эквивалентность
дизъюнкция
7.
Выберите правильный ответ. Используя логические высказывания А ="Это утро ясное", В= "Это утро теплое", выразите формулу А=>не В на обычном языке:
Это утро ясное или не тёплое
Если это утро ясное, то оно не тёплое
Если утро теплое, то оно и ясное
Это утро не ясное, но теплое
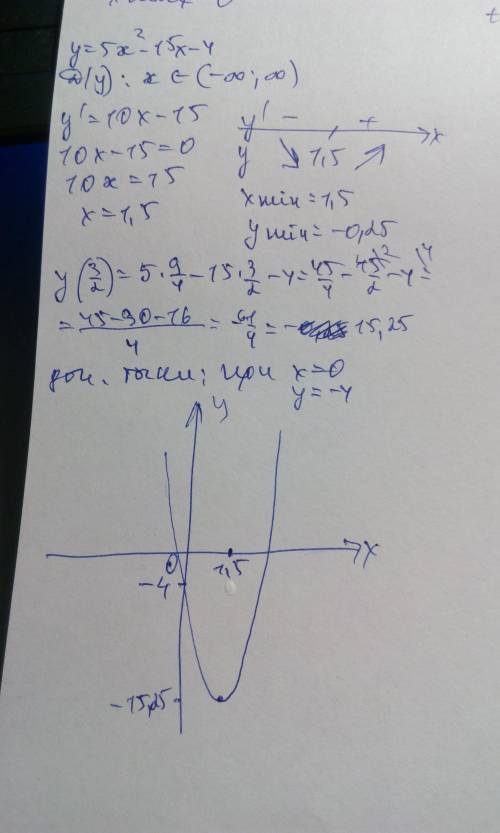
Пошаговое объяснение:
Всего вариантов последовательно выбрать три карточки: 8 * 7 * 6 (вытянули одну из восьми — осталось семь — затем осталось шесть).
A) Карточка с цифрой 1 может быть вытянута первой, второй или третьей. Тогда в каждом случае осталось семь карточек, а затем шесть: 1 * 7 * 6 + 7 * 1 * 6 + 7 * 6 * 1 = 3 * 7 * 6. Вероятность 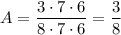
B) Чётная карточка может быть вытянута первой, второй или третьей, чётных цифр всего 4 (2, 4, 6, 8). Значит, существует четыре варианта вытянуть чётную карточку, затем остаётся четыре нечётных, затем — три нечётных. То есть подходящих вариантов 4 * 4 * 3 + 4 * 4 * 3 + 4 * 3 * 4 = 4 * 4 * 3 * 3. Вероятность 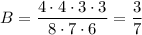
С) Сначала вытянули одну из четырёх нужных карточек, затем — одну из оставшихся трёх, затем — одну из оставшихся двух. Нужных вариантов: 4 * 3 * 2. Вероятность