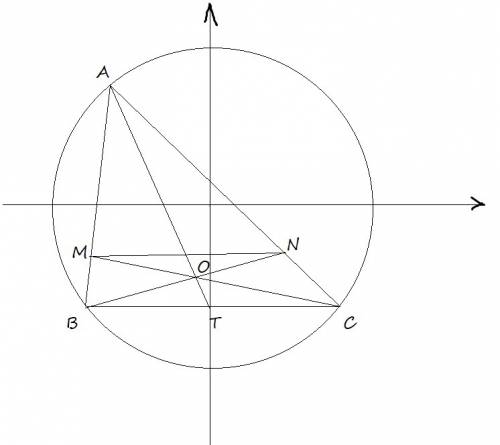
Поскольку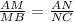 
, то треугольники MAN и BAC подобны. Значит MN параллелен BC ⇔ BMNC - трапеция. При этом BN и MC - диагонали. В трапеции отрезок, соединяющий середины оснований, продолжения боковых сторон и точка пересечения диагоналей лежат на одной прямой. Следовательно, AT - медиана треугольника ABC. Заметим, что отношение "расстояний" пройденных точками A и O равно искомому отношению диаметров окружностей, что равно отношению радиусов. Точка T зафиксирована. Спроецируем путь пройденный точкой O на вертикальную ось. Получим длину диаметра окружности. Данный диаметр пропорционален длине отрезка OT. Точка A пройдет весь путь окружности, проекция этого пути равна диаметру описанной окружности. Так как точка O лежит на отрезке AT, то пройденный путь пропорционален диаметру описанной окружности с тем же коэффициентом пропорциональности, что и отношение отрезка OT к соответствующему пути. Получили, что искомое отношение радиусов равно отношению 
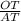. Пусть MB = x, AM = 3x; AN = 3y; NC = y; TC = BT; По теореме Менелая: 
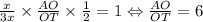, Значит 
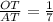; ответ: 7:1
8491,5372 округлить до тысяч 8000
8491,5372 округлить до сотен 8500
8491,5372 округлить до десятков 8490
8491,5372 округлить до единиц 8492
8491,5372 округлить до десятых 8491,5
8491,5372 округлить до сотых 8491,54
8491,5372округлить до тысячных 8491,537
Округлить число до определенной цифры (знака), значит, превратить все цифры справа от него в нули. Для того ,чтобы показать ,что число приблизительно равно округленному используют знак "≈"(приблизительно)
Правила округления:
Все цифры справа от той цифры (знака) до которой нужно округлить, превращаем в нули КРОМЕ ЕГО СОСЕДА СПРАВА.
Если сосед справа меньше 5, то цифра , до которой округляем, остается прежней.
Если сосед справа больше или равен 5, то к цифре ,до которой округляем, прибавляем 1.
360-30-100-130= 100° -искомый угол