(см. объяснение)
Пошаговое объяснение:
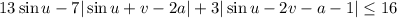
Введем замену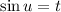 
. Откуда 
.
Тогда неравенство примет вид:
Пусть переменная здесь будет 
, а 
и 
параметры.
Наша задача определить, когда в решении этого неравенства будет содержаться промежуток ![[-1;\;1]](/tpl/images/2011/3499/001ed.png)
.
Заметим, что при любом раскрытии модулей перед буквой будет стоять положительное число.
Тогда при любых значениях параметров имеем возрастающую функцию 
.
Значит промежуток будет в решении неравенства, если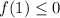 
, откуда переходим к новой записи:
Тогда пришли к неравенству:
Строим его в координатах 
и выделяем интересующую нас область:
(см. прикрепленный файл)
Итого при ![a\in\left[\dfrac{1}{5};\;\dfrac{3}{5}\right]](/tpl/images/2011/3499/9a62e.png)
исходное неравенство выполнимо для любой пары 
действительных чисел 
.
Задание выполнено!
21*340=7140
60993/753=81
7140-9567= - 2427
- 2427+576= -(2427-576)=-1851
-1851-81=-(1851+81)= -1932