Саму задачу можно переформулировать немного по-другому:
Было: Расставить минимальное количество шашек на шахматной доске 8 на 8, так чтобы было невозможно поставить коня так, чтобы он не бил ни одной шашки.Переходит в: расставить на доске минимальное количество коней так, чтобы было невозможно поставить шашку не под удар коня.Если мы решим вторую задачу, то просто нужно будет заменить коней шашками - и мы получим искомое расположение.
По поводу второй задачи можно заметить, что:
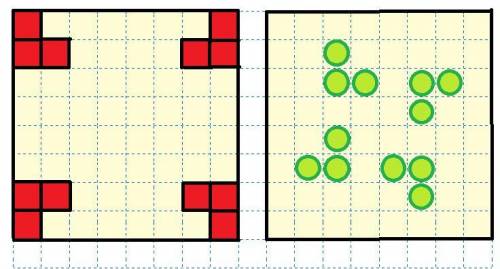
Разные кони должны бить выделенные красным клетки на рисунке ниже.Отсюда следует, что мы не можем расставить менее, чем 4 * 3 = 12 коней. Если это можно сделать, то задача решится. И да, это получилось сделать (рисунок 2).
Заменяем коней шашками и получаем ответ: 12 коней.
ответ: 12 шашек.
 и
и 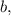 то ничего не изменится, всё будет работать как прежде.
то ничего не изменится, всё будет работать как прежде.
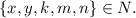
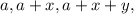 чтобы
чтобы![( [ a + 1 ] + x + y ) | ( 2a+x ) ,](/tpl/images/0497/6250/3dbb9.png)
![( [ a + 1 ] + x ) | ( 2a+x+y )](/tpl/images/0497/6250/bcfc5.png) и
и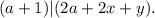
![k ( [ a + 1 ] + x + y ) = 2a + x](/tpl/images/0497/6250/3a31a.png) ;
;![(k-1) x + ky = 2a - k [ a + 1 ]](/tpl/images/0497/6250/d1c79.png) ;
;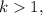 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.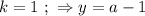 ;
;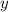 его значение
его значение 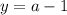 и будем искать такие комбинации
и будем искать такие комбинации 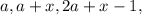 чтобы:
чтобы: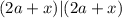 – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 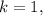
![( [ a + 1 ] + x ) | ( 3a+x-1 )](/tpl/images/0497/6250/b244e.png) и
и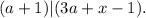
![m ( [ a + 1 ] + x ) = 3a+x-1](/tpl/images/0497/6250/c1228.png) ;
;![(m-1) x = 3a - 1 - m [ a + 1 ]](/tpl/images/0497/6250/be1b0.png) ;
;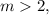 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.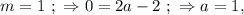 но это не подходит по условию.
но это не подходит по условию.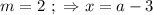 ;
; его значение
его значение 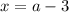 и будем искать такие комбинации
и будем искать такие комбинации 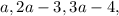 чтобы:
чтобы:![( 3 [ a - 1 ] ) | ( 3 [ a - 1 ] )](/tpl/images/0497/6250/de3e6.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 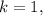
![( 2 [ a - 1 ] ) | ( 4 [ a - 1 ] )](/tpl/images/0497/6250/02549.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 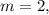
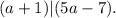
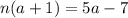 ;
;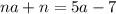 ;
; ;
;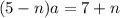 ;
;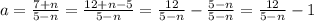 ;
;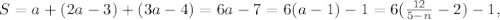
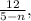 т.е. при
т.е. при 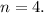
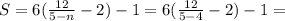
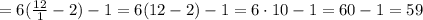 ;
;
0.48*х ---окуни, x --- целое число, 0.48х = (12х / 25) ---целое число))
т.е. х кратно 25: х=50 или х=75
25 ≤ х-5 ≤ 95
0.5*(х-5) ---окуни, это тоже целое число (нельзя поймать 1.4 окуня)
0.5*(75-5) = 35
ответ: 75 рыб поймал рыбак.