16 см; 16,24 см.
Пошаговое объяснение:
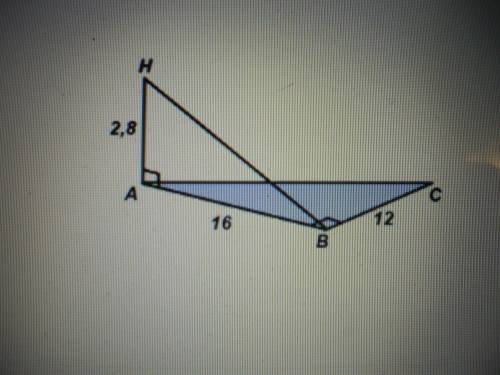
ΔАВС - прямоугольный, т.к. в условии сказано, что катеты равны 12 см и 16 см. Пусть АВ=16 см, ВС=12 см, ∠В=90°.
Меньший угол лежит напротив меньшего катета, значит меньший ∠А. ВН - расстояние до ВС от точки Н.
АВ ⊥ ВС как катеты, АВ - проекция наклонной ВН на плоскость ΔАВС, значит и ВН ⊥ ВС по теореме о трех перпендикулярах.
АН⊥АВС. Т.к. перпендикуляр является кратчайшим расстоянием между точкой и прямой, то расстояние от т. А до прямой ВС равно АВ=16 см.
Найдем ВН по теореме Пифагора из ΔАВН:
ВН=√(2,8²+16²)=√(2,8²+16²)=√(7,84+256)=√(263,84)≈ 16,24 см.
ответ: 16 см; 16,24 см.
629.
-48-52=-100
-9-16=-25
630.
-45*-5-45=225-45=180
-1*-1-13=1-13=-12
631.
-136-144=-280<-290
632.
-34-25-16=-169
633.
-2.27-0.73=-3
-0.08-1.94=-2.02
634.
-4.5-3.6=-8.1>-7.2
635.
-0.37-1.53-0.1=-2
636.
-4/5-2/3=-12/15-10/15=-22/15=-1 целая 7/15
-2/9-5/6=-4/18-15/18=-19/18=-1 целая 1/18
637.
-67/12-11/4=-67/12-33/12=-100/12=-8 целых 1/3
-11/8-17/6=-33/24-68/24=-101/24=-4целых 1/6
638.
(-27/8-17/4)+(-11/6-29/12)=(-27/8-34/8)+(-22/12-29/12)=-61/8+(-51/12)=-183/24-102/24=-285/24=-11 целых 21/24
Если что я везде перевела в обыкновенную дробь
Можно лувший ответ подааайлуста