Если я правильно понял задание, то требуется посчитать:
.
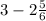Числитель - верхнее число в дроби.
Знаменатель - нижнее число в дроби.
В таком случае, следует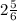 
перевести в неправильную дробь (2 умножить на знаменатель и прибавить числитель. Затем полученное число записать в числитель, оставив знаменатель неизменным).
Получится: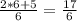 
Затем представим 3 в виде неправильной дроби со знаменателем 6 (3 умножим на знаменатель и полученное число поставим на место числителя, оставив знаменатель неизменным).
Получится: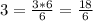 
Теперь посчитаем полученные дроби (считаем только числители при одинаковых знаменателях, оставляя сам знаменатель неизменным):
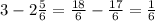
ответ: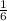 
.
АВСД - прямоугольник ⇒ ∠А=∠В=∠С=∠Д=90° .
Так как МА⊥ пл. АВСД ⇒ МА ⊥АВ , МА⊥АД , МА⊥АС.
Тогда треугольники АВМ , АДМ, АСМ, АДС, АДВ - прямоугольные , и к ним можно применить теорему Пифагора.
1)\; \; MB=\sqrt{AB^2+AM^2}=\sqrt{3^2+1^2}=\sqrt{10}2)\; \; MD=\sqrt{AD^2+AM^2}=\sqrt{4^2+1^2}=\sqrt{17}3)\; \; AC=\sqrt{AD^2+CD^2}=\sqrt{4^2+3^2}=54)\; \; BD=\sqrt{AD^2+AB^2}=\sqrt{4^2+3^2}=5\; ,\; \; AC=BD\; .
5)\; \; CM=\sqrt{AC^2+AM^2}=\sqrt{5^2+1^2}=\sqrt{26}6)\; \; S(MAC)=\frac{1}{2}\cdot AC\cdot AM=\frac{1}{2}\cdot 5\cdot 1=2,5
Пошаговое объяснение:
