Пусть дан правильный шестиугольник ABCDEF: AB = BC = CD = DE = EF = AF, AC = 12 см — меньшая диагональ.
1. Рассмотрим △ABC: ∠ABC = 120° (так как все углы правильного шестиугольника равны 120°). Так как AB = BC, то △ABC равнобедренный, тогда ∠BAC = ∠BCA = x.
По теореме о сумме углов треугольника:
∠ABC + ∠BAC + ∠BCA = 180°;
120° + x + x = 180°;
2 * x = 180° - 120°;
2 * x = 60°;
x = 60°/2;
x = 30°.
Таким образом, ∠BAC = ∠BCA = x = 30°.
2. По теореме синусов:
AC/sin∠ABC = AB/sin∠BCA;
12/sin120° = AB/sin30°;
12 : √3/2 = AB : 1/2;
12 * 2/√3 = AB * 2;
24/√3 = 2 * AB;
AB = 24/(2 * √3) = 12/√3 = 12√3/3 = 4√3 (см).
3. Радиус окружности, вписанной в правильный шестиугольник находится по формуле:
r = (√3 * a) / 2,
где a — длина стороны шестиугольника.
r = (√3 * 4√3) / 2 = (3 * 4) / 2 = 12/2 = 6 (см).
ответ: r = 6 см.
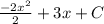
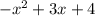
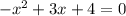
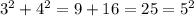
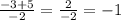
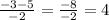
1) 15 3/4 * 2/3 = 63/4 * 2/3 = (21*1)/(2*1) = 21/2 = 10 целых 1/2 (км/ч) - скорость второго велосипедиста;
2) 15 3/4 + 10 1/2 = 15 3/4 + 10 2/4 = 25 5//4 = 26 1/4 (км/ч) - скорость сближения;
3) 26 1/4 * 4 = 105/4 * 4/1 = 105 (км) - расстояние между городами.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
то же самое в десятичных дробях
1) 15,75 * 2 : 3 = 10,5 (км/ч) - скорость другого велосипедиста;
2) 15,75 + 10,5 = 26,25 (км/ч) - скорость сближения;
3) 26,25 * 4 = 105 (км) - расстояние между городами.
ответ: 105 км.