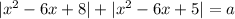
Рассмотрим две функции:
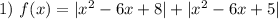
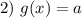 — линейная функция, график которой — прямая, параллельная оси абсцисс.
— линейная функция, график которой — прямая, параллельная оси абсцисс.
Изобразим данные функции на координатной плоскости.
Чтобы построить график функции 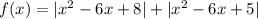 , следует раскрыть модуль на участках.
, следует раскрыть модуль на участках.
Найдем нули модулей функции 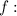
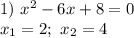
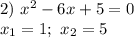
Рассмотрим функцию 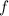 на пяти участках и раскроем модули в соответствии с участком (см. таблицу), используя правило:
на пяти участках и раскроем модули в соответствии с участком (см. таблицу), используя правило:
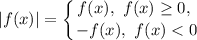
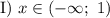

Построим график функции 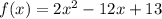 на участке
на участке 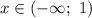 (см. пункт
(см. пункт 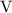 )
)
![\text{II}) \ x \in[1; \ 2]](/tpl/images/1356/5780/59dd4.png)
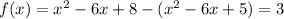
Построим график функции 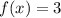 на участке
на участке ![x \in[1; \ 2]](/tpl/images/1356/5780/1fbb1.png)
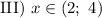
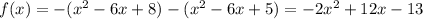
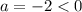 — ветви параболы направлены вниз
— ветви параболы направлены вниз
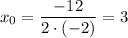
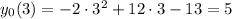
Пересечение с осями координат:
1) с осью абсцисс: 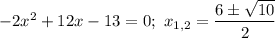
2) с осью ординат: 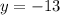
Построим график функции 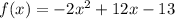 на участке
на участке ![x \in[1; \ 2]](/tpl/images/1356/5780/1fbb1.png)
![\text{IV}) \ x \in[4; \ 5]](/tpl/images/1356/5780/5caee.png)
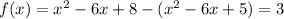
Построим график функции 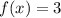 на участке
на участке ![x \in[4; \ 5]](/tpl/images/1356/5780/b98d5.png)
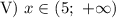

Построим график функции 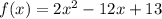 на участке
на участке 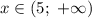
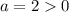 — ветви параболы направлены вверх
— ветви параболы направлены вверх
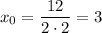
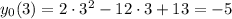
Пересечение с осями координат:
1) с осью абсцисс: 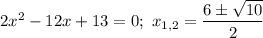
2) с осью ординат: 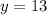
Изобразим график функции 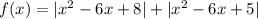 (см. рисунок).
(см. рисунок).
Уравнение 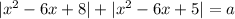 будет иметь более трех решений, если прямая
будет иметь более трех решений, если прямая 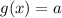 будет иметь более трех точек пересечения с графиком функции
будет иметь более трех точек пересечения с графиком функции 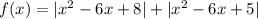
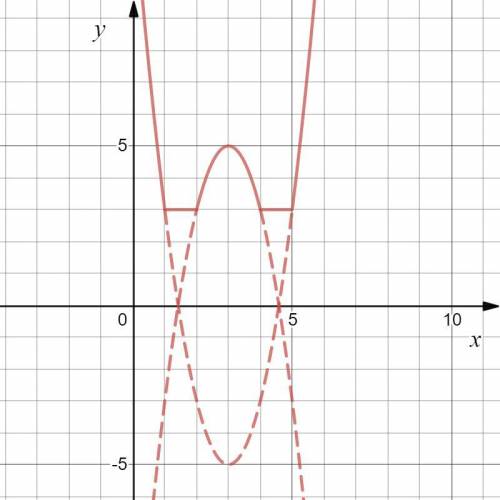
Изобразим возможные варианты решений (см. рисунок).
1) Если 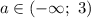 , то уравнение не имеет решений.
, то уравнение не имеет решений.
2) Если 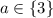 , то уравнение имеет множество решений (промежуток решений).
, то уравнение имеет множество решений (промежуток решений).
3) Если 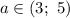 , то уравнение имеет 4 решения.
, то уравнение имеет 4 решения.
4) Если 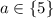 , то уравнение имеет 3 решения.
, то уравнение имеет 3 решения.
5) Если 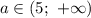 , то уравнение имеет 2 решения.
, то уравнение имеет 2 решения.
Таким образом, при 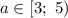 уравнение
уравнение 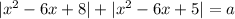 имеет более трех решений.
имеет более трех решений.
ответ: 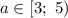

Пошаговое объяснение:
4.71
2x + Iax-5I = 0
запишем в виде Iax-5I = -2x
теперь получим первое и главное условие для решения х<0
и вот раскроем модуль
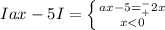
при любом раскладе 5/(а±2) должно быть <0, т.е при а> 2 решений нет
теперь рассмотрим первую строчку
ax-5 = 2x ⇒ х = 5/(а-2), при этом x<0, значит а-2<0, a<2
это мы нашли один интервал
теперь
ax-5 = 2x ⇒ х = 5/а+2, при этом x<0, значит а+2<0, a < -2
и теперь еще условие а≠ 2, т.к. знаменатель не может быть равен 0, т.е при а = 0 решений нет
ну вот, в общем-то и всё
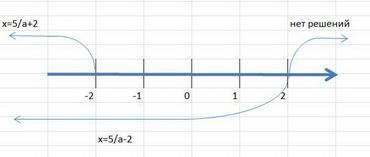
теперь нанесем все точки а и значения х на числовую ось и получим решение
a < -2 х = 5/а±2
-2 ≤a <2 х = 5/(а-2)
a ≥ 2 нет решения
(не совсем сходится с ответом, но в ответе есть ошибка. при a = -2
х не может быть равен 5/а+2, т.к. знаменатель будет 0
48-16=32
Второе ателье сшило на 32 костюма меньше