Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была 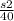 , а после встречи
, а после встречи 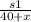 . Скорость второго пешехода до встречи и после встречи была одинаковой, значит
. Скорость второго пешехода до встречи и после встречи была одинаковой, значит  , откуда
, откуда  . У первого пешехода до встречи была скорость
. У первого пешехода до встречи была скорость  , а после встречи
, а после встречи 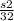 , скорость первого пешехода до встречи и после встречи была одинаковой, значит
, скорость первого пешехода до встречи и после встречи была одинаковой, значит 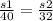 , откуда
, откуда 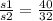 . По условию задачи составим уравнение
. По условию задачи составим уравнение .
.
1280+32х=1600
32х=320
х=10
ответ: После встречи второй пешеход придет в пункт А через 10 часов
Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была 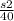 , а после встречи
, а после встречи 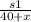 . Скорость второго пешехода до встречи и после встречи была одинаковой, значит
. Скорость второго пешехода до встречи и после встречи была одинаковой, значит  , откуда
, откуда  . У первого пешехода до встречи была скорость
. У первого пешехода до встречи была скорость  , а после встречи
, а после встречи 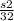 , скорость первого пешехода до встречи и после встречи была одинаковой, значит
, скорость первого пешехода до встречи и после встречи была одинаковой, значит 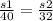 , откуда
, откуда 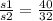 . По условию задачи составим уравнение
. По условию задачи составим уравнение .
.
1280+32х=1600
32х=320
х=10
ответ: После встречи второй пешеход придет в пункт А через 10 часов
56+490:х=63
490:х=63-56
490:х=7
х=490:7
х=70
2.
(d•8):2=240
d•8=240•2
d•8=480
d=480:8
d=60
3.
560:(13-х)+20=100
560:(13-х)=100-20
560:(13-х)=80
13-х=560:80
13-х=7
х=13-7
х=6
4.
(а:8+18)•6=360
(а:8+18)=360:6
(а:8+18)=60
а:8=60-18
а:8=42
а=42•8
а=336
5.
3•(500-а:3)=1320
(500-а:3)=1320:3
(500-а:3)=440
а:3=500-440
а:3=60
а=60•3
а=180