
dogmiroslava
14.02.2016
Алгебра
5 - 9 классы
+12 б.
ответ дан
Найдите область определения функции
а) y=√5x-4x^2 (всё выражение под квадрат. корнем)
б) y=√x^2+2x-80 (под квадрат. корнем) /3x-36
ОЧЕНЬ
2
ПОСМОТРЕТЬ ОТВЕТЫ
ответ, проверенный экспертом
5,0/5
0
axatar
главный мозг
2.4 тыс. ответов
548.5 тыс. пользователей, получивших
а) x∈[0; 1,25]
б) x∈(-∞; -10]∪[8; 12)∪(12; +∞)
Объяснение:
а)
Область определения функции:
подкоренное выражение должен быть неотрицательным
5·x-4·x²≥0
x·(5-4·x)≥0
Нули левой части неравенства
х=0 и 5-4·x=0 или х=0 и x=5/4=1,25
Применим метод интервалов
x·(5-4·x): - + -
-∞ -1 [0] 1 [1,25] 100 > +∞
То есть
при х= -1 : -1·(5-4·(-1)) = -1·(5+4) = -1·9 = -9<0
при х= 1 : 1·(5-4·1) = 1·(5-4) = 1·1 =1>0
при х= 100 : 100·(5-4·100)) = 100·(5-400) = 100·(-395) =-39500<0
ответ: x∈[0; 1,25]
б)
Область определения функции:
1) подкоренное выражение должен быть неотрицательным
x² + 2·x - 80≥0
Левую часть разложим на множители, для этого решаем как квадратное уравнение
D= 2²-4·1·(-80)=4+320=324=18²
x₁=(-2-18)/2= -20/2 = -10
x₂=(-2+18)/2= 16/2 = 8
(x - (-10))·(x-8)≥0
Нули левой части неравенства - это корни квадратного уравнения.
Применим метод интервалов
(x+10)·(x-8): + - +
-∞ -100 [-10] 0 [8] 100 > +∞
То есть
при х= -100: (-100+10)·(-100-8)) = -90·(-108) = 90·108 >0
при х= 0 : (0+10)·(-8)) = 10·(-8) = -80 <0
при х= 100 : (100+10)·(100-8)) = 110·92 >0
ответ: x∈(-∞; -10]∪[8; +∞)
2) знаменатель не должен быть нулем
3·x-36≠0 или 3·x≠36 или x≠12.
Тогда ответ: x∈(-∞; -10]∪[8; 12)∪(12; +∞)
1)
в) 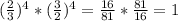
2)
а) 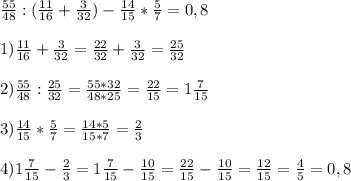
ответ: 0,8
б) 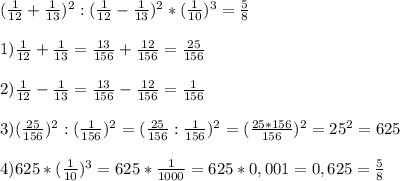
ответ: 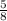
3)
1) 120 : 4 = 30 (задач) - составляет 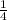 .
.
2) 120 - 30 = 90 (задач) - остаток.
3) 90 * 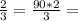 30*2 = 60 (задач)
30*2 = 60 (задач)
4) 120 - 30 - 60 = 120 - 90 = 30 (задач) - осталось решить.
ответ: 30 задач.
4) 1 - общее количество проданных тортов.
1) 1 - 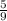 =
= 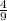 - продано после обеда.
- продано после обеда.
2) 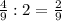 - составляют от общего 12 тортов.
- составляют от общего 12 тортов.
3) 12 : 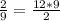 = 6*9 = 54 торта продано за день.
= 6*9 = 54 торта продано за день.
ответ: 54 торта.
5) Нужно привести 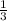 и
и 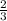 к общему знаменателю, кратному числу 13. Это число 39.
к общему знаменателю, кратному числу 13. Это число 39. 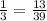 и
и 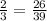 . Между ними находятся дроби:
. Между ними находятся дроби: 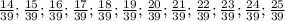 . 39 : 13 = 3, поэтому нужно искать дроби с числителем, кратным 3. Это дроби:
. 39 : 13 = 3, поэтому нужно искать дроби с числителем, кратным 3. Это дроби: 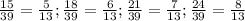 .
.
ответ: 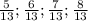 .
.