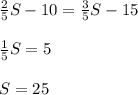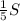 .
.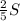 . В эту сумму входит сумма чисел верхнего левого квадрата 2х2, равная 10. Значит, сумма чисел в прямоугольнике высотой 2 и длиной 3 в верхнем правом углу равна
. В эту сумму входит сумма чисел верхнего левого квадрата 2х2, равная 10. Значит, сумма чисел в прямоугольнике высотой 2 и длиной 3 в верхнем правом углу равна 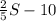 .
.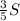 , и в которую входит нижний правый квадрат 3х3 с суммой 15. Уберём из этих нижних трёх строчек квадрат 3х3. Останется прямоугольник высотой 3 и длиной 2, по площади равный верхнему прямоугольнику 2х3, и в которых суммы чисел тоже равны. В нижнем оставшемся прямоугольнике сумма чисел равна
, и в которую входит нижний правый квадрат 3х3 с суммой 15. Уберём из этих нижних трёх строчек квадрат 3х3. Останется прямоугольник высотой 3 и длиной 2, по площади равный верхнему прямоугольнику 2х3, и в которых суммы чисел тоже равны. В нижнем оставшемся прямоугольнике сумма чисел равна 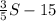 .
.