Боковые стороны трапеции равны по 8 см.
Пошаговое объяснение:
Трапеция называется равнобокой, если ее боковые стороны равны.
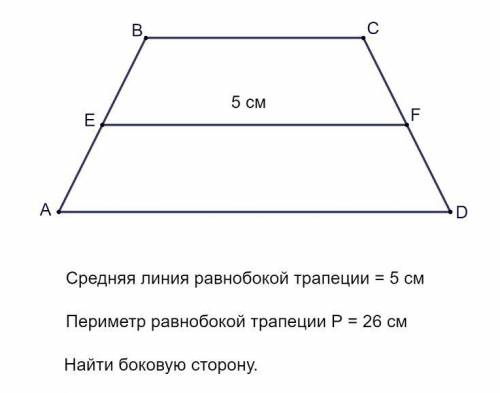
Пусть дана равнобокая трапеция ABCD. Ее боковые стороны равны AB = CD. Средняя линия EF = 5 см.
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции равна полусумме оснований.
EF =  см
см
BC + AD = 2 * 5 = 10 (см)
Периметр равен сумме длин всех сторон, P = 26 см.
Сумма боковых сторон трапеции: AB + CD = P - (BC + AD) = 26 - 10 = 16 (см).
Боковые стороны: AB = CD = 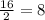 (см).
(см).
55×3(165) = 33×5 (165)
650+40(690) < 1000-170(830)
960÷3(320) = 1000-680(320)
1630+200(1830) > 1000-680(320)
650+40(690) > 33×5(165)
960÷3(320) < 410×2(820)
1000-170(830) > 55×3(165)