Реши в огороде собрали 65 кабачков, а огурцов на 17кг меньше. oгурцы разложили в пакеты по 6кг в каждый сколько пакетов огурцов получилось?

👇

Увидеть ответ

Ответ:

DontRobot

16.06.2020

65-17=48- огурцов
48:6=8 - разложили
ответ: 8 пакетов огурцов получилось.

4,8(91 оценок)

Открыть все ответы

Ответ:

vitaliygrg

16.06.2020

Пошаговое объяснение:

Дополни предложения.

Пешеход двигается с постоянной скоростью (v). Пройденный путь (s) –

переменная величина, время (t) –

переменная величина.

Периметр квадрата определяется по следующей формуле: P = 4a, где a – сторона квадрата и

переменная величина, а P – периметр и

переменная величина.

Площадь квадрата определяется по следующей формуле: S = a2, где S – площадь квадрата и

переменная величина, а его сторона a –

переменная величина.

Диаметр окружности (D) –

переменная величина, а ее радиус (R) –

переменная величина.

Объем работы (A), выполненной за 3 часа, –

переменная величина, а производительность труда –

переменная величина.

Цена одной тетради –

переменная величина, а стоимость 5 тетрадей –

переменная величина.

4,4(1 оценок)

Ответ:

Лейла011

16.06.2020

Последовательности удовлетворяющие условию будем называть "правильными". Любая правильная последовательность начинается с +1 (по условию) и заканчивается на -1 (иначе $a_1+a_2+\ldots+a_{2n-1}< 0$ ).

Правильную последовательность длины 2n можно получить так:
1) Выбрать произвольное k с условием 0≤k≤n-1.
2) Между 1 и -1 вставить любую правильную последовательность длиной 2k.
3) К полученной последовательности приписать правильную последовательность длиной 2(n-k-1). При этом, если надо приписывать или вставлять последовательность нулевой длины, то ничего не делаем.
В итоге, получается последовательность длиной 2+2k+2(n-k-1)=2n. Причем, эта последовательность обязательно правильная, т.к.
a) $a_1+a_2+\ldots+a_{j}\ge 1$ при 1≤j≤2k+1 (т.к. после начальной 1 мы приписали правильную длиной 2k)
б) $a_1+a_2+\ldots+a_{j}= 0$ при j=2k+2 (т.к. сумма всех элементов правильной равно 0 и сумма 1 и -1 тоже 0)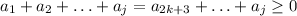
в) $a_1+a_2+\ldots+a_{j}=a_{2k+3}+\ldots+a_{j}\ge 0$ при 2k+3≤j≤2n (при k=n-1 этой части нет).
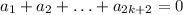Обратное тоже верно. Любую правильную последовательность длины 2n можно представить в таком виде. Действительно, в качестве k можно выбрать первое такое k, что $a_1+a_2+\ldots+a_{2k+2}= 0$ . Тогда a_1=1

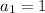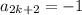, $a_{2k+2}=-1$ , а все последовательные суммы элементов между ними больше или равны 0, т.к. все суммы начиная с первой единицы больше или равны 1 (не забываем, что мы выбрали ПЕРВОЕ такое k). Т.е. между 1 и -1 находится правильная последовательность длины 2k. Все, что находится после этих 2k+2 элементов, очевидно, также является правильной последовательностью.Таким образом, для произвольной правильной последовательности длины 2n выполнены все условия а), б), в).

Из этого построения следует рекуррентная формула для числа всех правильных последовательностей длины 2n. Обозначим через c_k

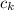число правильынх последовательностей длины 2k. Тогда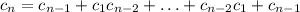
$c_{n}=c_{n-1}+c_1c_{n-2}+\ldots+c_{n-2}c_1+c_{n-1}$
Здесь первое слагаемое соответствует k=0, т.е.это количество всех правильных последовательностей вида {1,-1, произвольная правильная последовательность длины 2(n-1)}.
Второе слагаемое соответствует k=1, когда последовательности имеют вид
{1, все правильные последовательности длины 2, -1, все правильные последовательности длины 2(n-2)}. И т.д.
Итак, для n=7:
c_1=1

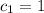(такая последовательность всего одна: {1,-1})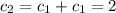
c_2=c_1+c_1=2

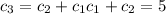
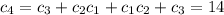
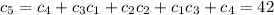
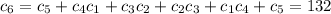
c_6=c_5+c_4c_1+c_3c_2+c_2c_3+c_1c_4+c_5=132

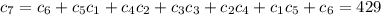
c_7=c_6+c_5c_1+c_4c_2+c_3c_3+c_2c_4+c_1c_5+c_6=429

ответ: 429.

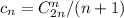P.S. Полученное рекуррентное соотношение можно упростить, и доказать, что $c_n=C_{2n}^n/(n+1)$ . Это можно доказать по индукции, или с производящих функций. Сама задача эквивалентна задаче о количестве правильных расстановок 2n скобок (n открывающих и n закрывающих). Открывающая скобка соответствует +1, и закрывающая соответствует -1. (число открывающих скобок левее k-oй позиции не меньше числа закрывающих). Количество таких расстановок называется числом Каталана. Есть еще множество интересных переформулировок этой задачи. Все можно найти в интернете по запросу "Числа Каталана".