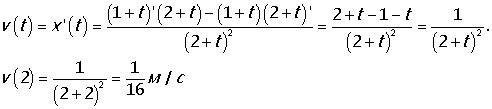
Пошаговое объяснение:
4.71
2x + Iax-5I = 0
запишем в виде Iax-5I = -2x
теперь получим первое и главное условие для решения х<0
и вот раскроем модуль
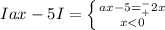
при любом раскладе 5/(а±2) должно быть <0, т.е при а> 2 решений нет
теперь рассмотрим первую строчку
ax-5 = 2x ⇒ х = 5/(а-2), при этом x<0, значит а-2<0, a<2
это мы нашли один интервал
теперь
ax-5 = 2x ⇒ х = 5/а+2, при этом x<0, значит а+2<0, a < -2
и теперь еще условие а≠ 2, т.к. знаменатель не может быть равен 0, т.е при а = 0 решений нет
ну вот, в общем-то и всё
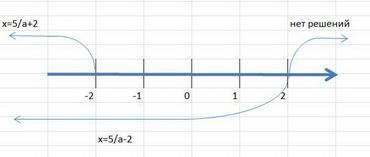
теперь нанесем все точки а и значения х на числовую ось и получим решение
a < -2 х = 5/а±2
-2 ≤a <2 х = 5/(а-2)
a ≥ 2 нет решения
(не совсем сходится с ответом, но в ответе есть ошибка. при a = -2
х не может быть равен 5/а+2, т.к. знаменатель будет 0
lg | (x² - x - 1) / (x² + x - 2)| = 0
одз
модуль всегда не отрицателен, значит надо проверить чтобы знаменатель не равнялся 0
x² + x - 2 ≠0 D=1 + 8 = 9 x12 ≠ (-1+-3)/2 ≠ -2 1
и тело логарифма не равнялась 0
x² - x - 1 ≠ 0 D=1 + 4 = 5 x34=(1 +- √5)/2 ≠ (1+√5)/2 (1-√5)/2
===
| (x² - x - 1) / (x² + x - 2)| = 1
1. (x² - x - 1) / (x² + x - 2) = 1
x² - x - 1 = x² + x - 2
2x = 1
x = 1/2
2. (x² - x - 1) / (x² + x - 2) = -1
x² - x - 1 = -x² - x + 2
2x² - 2x - 3 = 0
D = 4 + 4*2*3 = 28
x23 = (2 +- √28)/4 = (1 +- √7)/2
ответ (1 +- √7)/2, 1/2