(см. объяснение)
Пошаговое объяснение:
Поскольку в условии не дано основание логарифма, то примем его равным 10. При другом его численном значении логика решения не поменяется.
Первый :
Заметим, что если x - корень уравнения, то -x тоже. Тогда единственное решение возможно, если x=0.
При этом значении переменной найдем параметр:
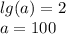
Покажем, что при нем у уравнения нет других корней:
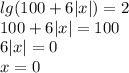
(здесь ОДЗ не пишем, так как преобразованиями оно гарантируется)
Тогда такое значение параметра подходит.
Второй :
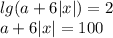
Из этой строки следует, что условие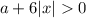 
всегда выполняется.
Решим параметр в координатах (x; a):
Выполним построение:
(см. прикрепленный файл)
Откуда следует, что ответом будет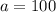 
.
Задание выполнено!
На данном уроке мы начнём изучение темы Неопределенный интеграл, а также подробно разберем примеры решений простейших (и не совсем) интегралов. В этой статье я ограничусь минимумом теории, и сейчас наша задача – научиться решать интегралы.
Что нужно знать для успешного освоения материала? Для того чтобы справиться с интегральным исчислением Вам необходимо уметь находить производные, минимум, на среднем уровне. Поэтому, если материал запущен, то рекомендую сначала внимательно ознакомиться с уроками Как найти производную? и Производная сложной функции. Не лишним опытом будет, если у Вас за плечами несколько десятков (лучше – сотня) самостоятельно найденных производных. По-крайне мере, Вас не должны ставить в тупик задания на дифференцирование простейших и наиболее распространенных функций. Казалось бы, при чем здесь вообще производные, если речь в статье пойдет об интегралах?! А дело вот в чем. Дело в том, что нахождение производных и нахождение неопределенных интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия, как, например, сложение/вычитание или умножение/деление. Таким образом, без навыка (+ какого-никакого опыта) нахождения производных, к сожалению, дальше не продвинуться.
